Hvorfor regne med bokstaver?

Algebra er nyttig da den gir oss generelle løsningsmetoder. Vi får verktøy til å løse flere liknende problemer raskt og effektivt i stedet for å jobbe med hvert problem helt fra bunnen av.

Nå skal vi se på et par eksempler som viser fordeler til algebra.

Eksempel 1

Arealet av et rektangel med bredde b og lengde l er som kjent $A = b \cdot l$ .

Arealet til et rektangel med sidelengde $b = 5$ cm og $l = 10$ cm er lik

$A = 5 \cdot 10 {c m}^{2} = 50 {c m}^{2}$ .

Arealet til et rektangel som er 4 cm bred og 6 cm lang, er lik

$A = 4 \cdot 6 {c m}^{2} = 24 {c m}^{2}$ .

Her ser vi et eksempel på at så lenge vi kjenner lengden og bredden til et rektangel kan vi ved hjelp av formelen $A = b \cdot l$ regne ut arealet av et hvilket som helst rektangel.

Eksempel 2

Hvor lang strekning tilbakelegger vi hvis vi kjører 60 km/h i en og halv time?

Sammenhengen mellom tilbakelagt strekning $s$ ved konstant fart, $v$ , etter tid, $t$ , er gitt ved;

$s = v \cdot t$

Alt vi trenger å gjøre er å sette inn for $v$ og $t$ i formelen:

$s = v \cdot t = 60 k m / h \cdot 1, 5 h = 90 k m$

Formelen vi bruker forteller oss at hvis vi beveger oss i konstant fart, er strekningen vi legger igjen bak oss lik farten multiplisert med tiden. Denne formelen gjelder for alle slike tilfeller siden det igjen er skrevet på en generell form med bokstaver. Dersom vi setter inn andre verdier for $v$ og $t$ , vil vi få forskjellige verdier for $s$ også.

Del på Facebook

Del på Facebook

Lynkurs, 8.-10.trinn

Algebra

Består av:

Begrep

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².
Fart

Fart er tilbakelagt distanse per tidsenhet.

Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.

Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.
Lengde

Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.
Multiplikasjon

Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".

Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.

Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.

Eksempel: 3 · 4 = 12 og 4 · 3 = 12

Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).
Rektangel

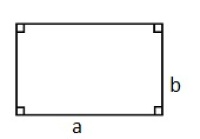
Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

Hvorfor regne med bokstaver?

Eksempel 1

Eksempel 2

Lynkurs, 8.-10.trinn

Algebra

Består av:

Begrep

Areal

Fart

Lengde

Multiplikasjon

Rektangel