Når kan vi legge sammen prosenter?
Det kan være fristende å legge sammen prosenter på samme måte som andre tall, men det blir ikke alltid riktig. Hvorfor?
Repetisjon
Prosent betyr en hundredel av det hele, altså er . Når vi regner med prosent, betyr det å finne prosent av noe, av det hele.
Du får tilbud om å få enten av tusen kroner eller 1% av en million kroner. Hvilket tilbud gir deg mest penger? En prosent av tusen kroner er en hundredel av tusen kroner, altså kroner. En prosent av en million er en hundredel av en million, altså kroner. Så selv om begge tilbud er , er antallet kroner du får veldig forskjellig. Grunnen til dette er at prosenten er en del av to ulike pengesummer.
Du skal bake muffins. Halvparten, , av muffinsene skal du ta med deg på skolen. Hvor mange muffins er eller halvparten? Umulig å si så lenge vi ikke vet totalt antall muffins du baker. Hvis du baker muffins, vil være . Baker du muffins, vil være muffins. Igjen ser vi at selv om vi skal finne , betyr det at vi må vite det totale antallet først. Hvis det hele er forskjellig, vil også antallet som svarer til prosenten være forskjellig.
La oss nå se på tilfeller der vi skal legge sammen prosenter.
Eksempel 1. Forskjellig helhet
På skolen International er det to klasser med elever i hver. I den ene klassen er det svensker og i den andre er det dansker. Hvor stor prosent svensker og dansker er til sammen i disse to klassene?
Legg merke til at det er prosenter av to forskjellige klasser.
er det samme som . En femtedel av elever er elever. Se på bildet.
| av en klasse på elever utgjør 5 personer . |
Vi skal se på antallet svensker og dansker til sammen. I de to klassene har vi svensker og dansker, til sammen elever. I de to klassene er det til sammen elever. På figuren under har vi fargelagt av elever. Nå regner vi ut hvor mange prosent av elever er:
Svar: Det er svensker og dansker til sammen i disse to klassene.
| Vi ser at vi IKKE kan svare at det er svensker og dansker til sammen i de to klassene! Grunnen til dette er at helheten vi tar prosent av forandrer seg fra til elever. |
regel
Prosenter kan legges sammen bare hvis begge er prosenter av samme helhet.
Eksempel 2. Samme helhet
I en klasse på elever er av elevene svenske og er danske. Hvor stor prosent svensker og dansker er det til sammen i klassen? Vi antar at ingen er svenske og danske.
av personer er personer. Det er svenske og danske elever, til sammen av . av elever utgjør
,
så vi ser at
i dette tilfellet.
Svar: Til sammen er det svensker og dansker i klassen.
| Det skraverte feltet representerer igjen både svenske og danske elever. |
I dette eksempelet ser vi at helheten ( elever) er den samme hele tiden, og derfor får vi ikke problemet fra det forrige eksempelet.
Del på Facebook
Begrep
-
Brøk
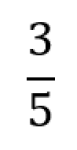
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.Eksempel : . Tallet 7 er nevneren.
-
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
-
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.







