Å fullføre kvadratet
Et kvadrat (ofte kalt fullstendig kvadrat) er et uttrykk som står i 2. potens, altså et uttrykk på formen , der innholdet i parentesen kan være hva som helst. Når vi har et andregradsuttrykk, altså et uttrykk der deler av det (men kanskje ikke hele) står i 2. potens, er det ofte nyttig å skrive om uttrykket slik at det ligner mest mulig på et fullstendig kvadrat. Dette kalles å fullføre kvadratet. Ved hjelp av dette kan vi skrive om et annengradsuttrykk som til noe på formen , der er en konstant. Vi får altså fjernet det lineære leddet , noe som viser seg å ha mange fordeler.
Hvordan gjør vi så dette i praksis? Faktisk er alt vi trenger følgende enkle utregning:
|
Metoden med å fullføre kvadratet La være et tall. Da er
|
Legg merke til at det eneste som skjer i utregningen, er at vi legger til og trekker fra . Resten følger direkte fra 1. kvadratsetning. Regn gjerne over dette selv. Regelen er grei nok, men man må øve litt på å bruke den, så vi ser på noen eksempler.
Eksempel 1
Skriv uttrykket på formen , der er en konstant.
Dersom vi skriver koeffisienten foran som i stedet for 10, ser de to
første leddene i uttrykket ut som
Dette uttrykket har samme form som venstresiden i metoden over, med . Vi prøver derfor å legge til og trekke fra . Vi får da at uttrykket vi startet med blir lik
|
|
Dermed fikk vi skrevet uttrykket på formen , med og .
Eksempel 2
Løs likningen for ved først å lage et fullstendig kvadrat på venstre side.
For å slippe koeffisienten foran -leddet, deler vi likningen på 2:
Poenget er nå å fullføre kvadratet på venstresiden ved å legge til et passende tall på begge sider av likhetstegnet. I likningen er , så og vi vil legge til for å fullføre kvadratet. Utregningen blir slik:
Eksempel 3
Faktoriser uttrykket .
Vi lager et fullstendig kvadrat av ved å legge til og trekke fra
Dette uttrykket lar seg faktorisere ved konjugatsetningen:
| . |
Resultatet blir altså at
Del på Facebook
Begrep
-
Andre kvadratsetning
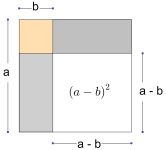
Andre kvadratsetning sier at
.
-
Første kvadratsetning
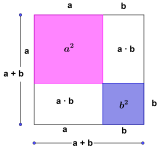
Første kvadratsetning sier at
.
-
Konjugatsetningen
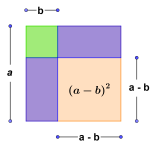
Konjugatsetningen kalles også tredje kvadratsetning:
.
-
Perfekt kvadrat
Et perfekt kvadrat er et uttrykk som kan skrives som , altså at det er et eller annet i andre potens.




