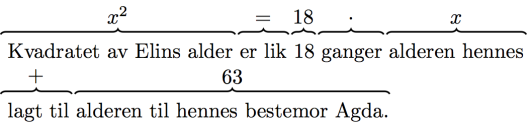Uoppstilte andregradslikninger

Areal

Arealberegninger vil involvere produkter – benevningen på areal er jo "’kvadrat-et-eller-annet," og arealproblemer gir oss ofte kvadratiske relasjoner.

Arealet av et kvadrat er $36m^2$. Finn lengden av sidene i kvadratet.

Vi kan i dette tilfellet finne svaret 6 uten for mye strev, men la oss kalle lengden på sidene i kvadratet for x. Ved å bruke formelen for arealet av et kvadrat med sidelengde x kan vi fra teksten sette opp likningen

som har løsninger $\pm 6$. Siden vi skal ha tak i en lengde (som ikke kan være negativ), er det 6 som er svaret vi søker.

Her ser vi også en annen ting vi må være bevisste på: Den matematiske modellen stemmer ikke alltid helt med virkeligheten. Derfor kan vi ikke bare plugge inn tallene og skrive ned svaret, vi må også tenke over hva det vi får betyr tilbake i det problemet vi begynte med. Hvis oppgaven over var første ledd i å bygge et gjerde og vi sa at vi hadde sidekanter på $-6$ meter hadde nok ingen blitt så imponert over oss...

En aldernøtt

Å komme seg fra tekst til matematikk kan være vanskelig. I dette eksempelet skal vi bare sette opp likningen (som du kan få løse selv).

Kvadratet av Elins alder er lik 18 ganger alderen hennes lagt til alderen til hennes bestemor Agda. Bestemor Agda er 63 år. Hvor gammel er Elin?

Vi lar $x$ være alderen til Elin (den ukjente størrelsen i problemet), og setter inn matematiske symboler istedenfor tekst:

Det gir likningen

som er en andregradslikning.