Rasjonale ulikheter
Den mest avanserte typen ulikhet vi skal se på i dette kurset er den rasjonale ulikheten. Dette er uttrykk der vi har en brøk med x i både over og under brøkstreken.
Først et viktig poeng: Hittil har vi sett på å løse ulikheter der høyresiden er 0. Hva om det står noe annet der? Jo, da bruker vi regnereglene for ulikheter og skriver om slik at det står 0 på høyresiden, og så kan vi gjøre slik vi har gjort hittil. Her viser vi et eksempel hvor vi vil løse en rasjonal ulikhet:
Vi flytter over 1:
| , |
og setter på felles nevner. Det gir i telleren, som
etter opprydding gir ulikheten (sjekk!):
| . |
Rasjonale ulikheter løser vi på samme måte som de andre: Vi drøfter hver faktor for seg og slår dem sammen. Fortegnene vil følge samme multiplikasjonstabell som for
produkter, selv om faktorene nå er dividender og/eller divisorer. Den eneste
forskjellen er at nevneren ikke kan være 0. Det markerer vi gjerne i skjemaet
med et kryss for de -ene som gjør at nevneren er 0.
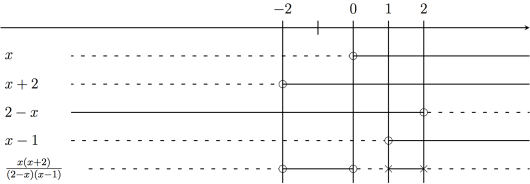
Når vi gjør dette får vi følgende fortegnsskjema:
Løsningene til ulikheten er dermed eller eller . (Siden ulikheten ikke er streng, er endepunktene og med. Setter vi for eksempel inn i ulikheten, får vi , som stemmer. Endepunktene og er ikke med siden de gir i nevneren til uttrykket.)
Del på Facebook
Lynkurs 11.-13.trinn
Ulikheter
Består av:
- Lineære ulikheter
- Uoppstilte ulikheter
- Fortegnsskjema
- Ulikheter av høyere grad
- Rasjonale ulikheter
Begrep
-
Fortegnsskjema
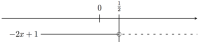
Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.