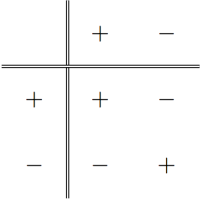Fortegnsskjema
Når vi arbeider med uttrykk i x er det noen ganger viktig å svare på spørsmål som: For hvilke verdier av x er uttrykket positivt? Lik 0? Negativt? For eksempel, hvis vi har et uttrykk for temperatursvingninger: Når er temperaturen positiv? Lik 0? Negativ? Når vi svarer på denne typen spørsmål sier vi at vi drøfter fortegnet til uttrykket.
Førstegradsuttrykk
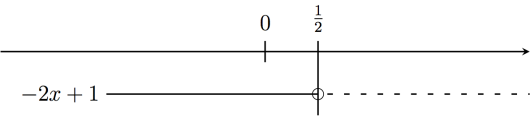
Når er for eksempel det lineære uttrykket positivt? lik 0? negativt? Ved å løse den lineære likningen finner vi at uttrykket er 0 når . Ved å løse ulikheten , ser vi at uttrykket er (strengt) positivt for , og ved å snu ulikheten, ser vi at det er negativt for .
Vi kan tegne opp fortegnsskiftet for et lineært uttrykk i med en såkalt fortegnslinje. Vi tegner først opp
Tallinje
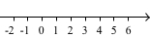
En rett linje der hvert punkt korresponderer til et tall og ethvert tall svarer til et punkt på linjen.
Uttrykket i eksempelet over gir fortegnslinja:
Et generelt lineært uttrykk i x er på formen der a og b er konstante tall. Dette uttrykket er lik 0 når . Videre har vi følgende(sjekk og tegn!):
• Hvis , skifter uttrykket fortegn fra til når .
• Hvis , skifter uttrykket fortegn fra til når .
Andregradsuttrykk
Hvordan varierer så fortegnet til et andregradsuttrykk? Når er positivt? Lik 0? Negativt?
Her er det en stor fordel å kunne faktorisere! Vi faktoriserer andregradsuttrykket i lineære faktorer (hvis mulig), og fortegnsdrøfter hver lineær faktor. Deretter ser vi på fortegnet til produktet, og bruker at produktet av et positivt tall og et negativt tall er negativt, mens produktet av to positive tall er positivt, og produktet av to negative tall er positivt (egenskaper ved de reelle tallene igjen). Det gir denne "multiplikasjonstabellen":
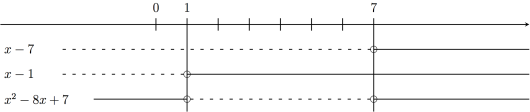
Når er uttrykket positivt? Lik 0? Negativt? Vi faktoriserer uttrykket:
Faktoren er lik 0 for , positiv for og negativ for .
Faktoren er lik 0 for , positiv for og negativ for .
(Hvis for eksempel , er negativ, mens er positiv, dermed er produktet negativt for .) Hvis vi slår sammen fortegnene på faktorene, får vi at er lik 0 for og , positivt for og og negativt for .
Vi kan tegne opp fortegnsskiftet for andregradsuttrykk i et fortegnsskjema:
For hver lineær faktor tegner vi fortegnslinja til faktoren, og til slutt lager vi
en fortegnslinje for uttrykket, ved å følge ’multiplikasjonstabellen’ over.
Fortegnsskjemaet for uttrykket er:
Del på Facebook
Begrep
-
Faktorisering av uttrykk
Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.
Eksempel:
-
Fortegnsskjema
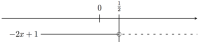
Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.