Enhetssirkel
Hva er en enhetssirkel?
definisjon
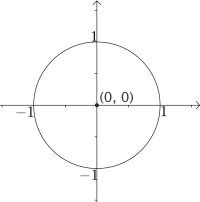
Enhetssirkelen er sirkelen i planet med radius og sentrum i origo, det vil si i punktet .
Vi vet at omkretsen til denne sirkelen er . Vi definerer dermed en full omdreining til å være radianer: det vil si at antall radianer alltid er lengden av sektoren på enhetssirkelen spent ut av vinkelen!
Eksempel 1
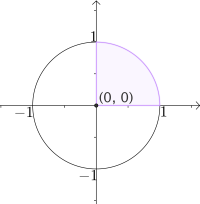
På bildet har vi fargelagt første kvadrant av enhetssirkelen. Vi vet at denne har lengde . Men vi vet også at den tilsvarende vinkelen er på . Dermed er .
Eksempel 2
La være en sirkel med sentrum i origo og radius og la være en vilkårlig sektor på spent ut av en vinkel på radianer. Finn lengden av .
Da er en full omdreining, vet vi at sektoren spent ut av en vinkel på er en halvsirkel. Dermed blir svaret omkretsen delt på to: .
teorem
La være en sirkel med radius og la være en sektor av spent ut av en vinkel på radianer. Da kan vi regne ut lengden av ved formelen
Bevis
Definisjonen av radianer er lengden av den assosierte sirkelsektoren på en sirkel med radius . Formelen for omkretsen av en sirkel (eller mer passende for vårt tilfelle, sirkelsektoren spent av radianer), , viser at lengden til sektoren er proposjonal med radiusen av sirkelen.
Del på Facebook