Regresjon 2: hva betyr det at en kurve «passer til dataene»?

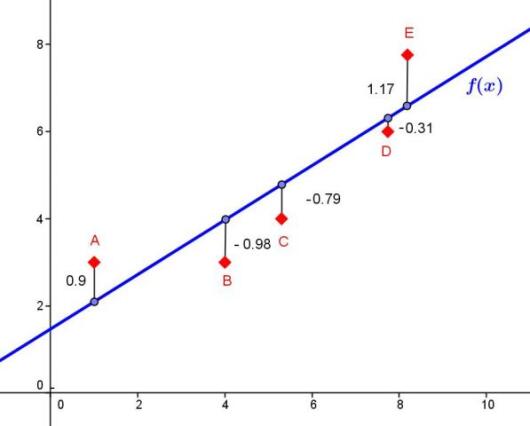
Vi har et sett med observasjoner og en lineær funksjon som skal passe til dataene, slik figuren under viser.

På figuren har vi tegnet inn vertikale linjer fra punktene og opp eller ned til funksjonen. Vi har også markert lengden på disse linjene. Disse lengdene sier vi er avstanden fra et punkt til funksjonen. For et bestemt punkt $\left(x,y\right)$ vil avstanden til funksjonen være $y-f\left(x\right)$.

Vi vil summere opp disse avstandene, feilen, for å få et mål på hvor godt funksjonen passer. Men, legg merke til at avstanden kan være både positiv og negativ. Det blir feil hvis vi trekker fra en avstand bare fordi feilen er «på nedsiden». Løsningen er å opphøye alle avstandene i andre, da blir alt positivt. Dette kaller vi kvadratsummen:

${\left(0,9\right)}^2+{\left(-0,98\right)}^2+{\left(-0,79\right)}^2+{\left(-0,39\right)}^2+{\left(1.17\right)}^2=3,86$

Generelt er kvadratsummen for data $\left(a_1,b_1\right),\left(a_2,b_2\right),\cdot \cdot \cdot ,\left(a_n,b_n\right)$ og en funksjon $f\left(x\right)$

${\left(b_1-f\left(a_1\right)\right)}^2+{\left(b_2-f\left(a_2\right)\right)}^2+\cdot \cdot \cdot +{\left(b_n-f\left(a_n\right)\right)}^2$

Vi kan bruke kvadratsummen for å sammenlikne hvor godt forskjellige funksjoner passer til et datasett. Jo nærmere null, jo bedre er det. Legg merke til at definisjonen av kvadratsummen fungerer like godt for andre funksjoner som ikke er lineære.

Kommentar: Hvis du bruker kalkulator, får du ofte opp et tall «r=». Dette er en annen måte å måle hvor godt kurven passer til observasjonene. Den kalles korrelasjonskoeffisienten. Hvis korrelasjonskoeffisienten er nær 1 eller -1 har vi en godt tilpasset kurve.