Regresjon 1

Vi har et sett av observasjoner, for eksempel mengde nedbør og antall mennesker i en handlegate på forskjellige dager. Vi kan tegne opp observasjonene våre i et koordinatsystem der vi lar x-aksen angi hvor mye nedbør det er og y-aksen hvor mange mennesker det er i handlegata.  Regresjon er da kort sagt det å finne en funksjon, $f\left(x\right)$, som passer best mulig til de observerte dataene, altså slik at kurven er nærmest mulig punktene våre.

Grunnen til at vi vil finne funksjonen $f\left(x\right)$ er at vi vil kunne si noen generelt om sammenhengen observasjonene viser. Hva slags mønstre finnes? Øker observasjonene sammen, eller minker den ene når den andre øker? Ved å finne en funksjon kan vi også gi prediksjoner om framtiden.

Hva slags funksjon $f$ skal være, kommer an på hva slags data vi ser på. I eksempelet under kan vi se at dataene ser ut til å ligge på en linje, og da vil vi gjerne finne en lineær funksjon, altså en funksjon på formen $f\left(x\right)=ax+b$.  Denne funksjonen finner vi da ved hjelp av kalkulator, regneark, GeoGebra eller andre hjelpemidler. Andre ganger kan det være at vi leter etter en eksponentiell funksjon, $f\left(x\right)=a{e}^{bx}$, eller en andregradsfunksjon, $f\left(x\right)=a{x}^2+bx+c$, eller kanskje en trigonometrisk funksjon, $f\left(x\right)=a\sin \left(bx\right)+d\cos \left(cx\right)$. For å finne den beste funksjonen, prøver man gjerne litt forskjellige funksjoner.

Eksempel

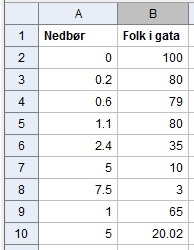
Vi har som data følgende observasjoner av mengde nedbør på en dag og antall mennesker i en handlegate. Vi vil finne en lineær funksjon som beskriver mønsteret i observasjonene.

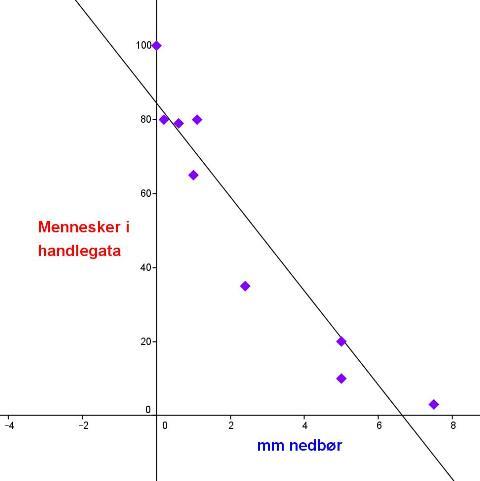
Her har vi brukt GeoGebra til å tegne punktene, og så brukt regresjonsfunksjonen til å finne en lineær funksjon som passer best mulig til punktene.

Funksjonen vi kom fram til her er $f\left(x\right)=-12,71x+84,65$.

Nå kan vi gjøre prediksjoner om framtiden: Ut ifra modellen vi fant, hvor mange mennesker vil du forvente er i gata hvis det er 4 mm nedbør?

Svar: Vi leser av på 4 mm og finner at vi vil ha ca. 34 mennesker i gata. Dette kan du også finne ved å sette inn $x=4$ i funksjonen over.

Denne prediksjonen må vi imidlertid ta med en klype salt. Vi har basert modellen vår på 9 datapar, og det er ikke så mye.

Ikke-lineær regresjon

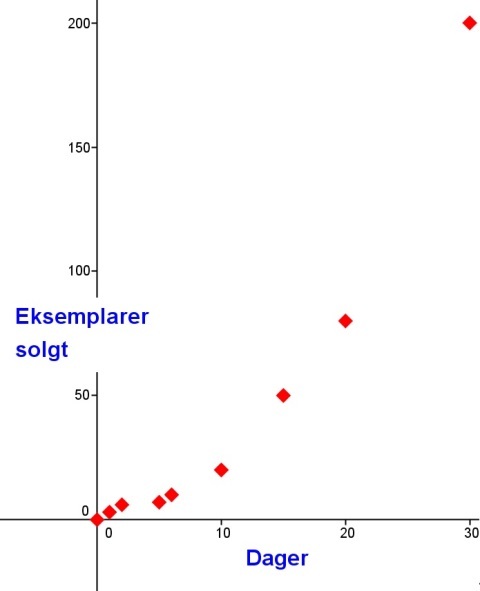
Det er imidlertid ikke alltid at en rett linje, en lineær funksjon, passer best til dataene våre. I eksempelet under har vi data fra en salget av en ny vare mot antall dager varen har vært på markedet. Vi ser at den selger lite de første dagene, men så skyter salget fart.

Vi ser at en lineær funksjon vil passe dårlig i dette tilfellet, men at en eksponentiell funksjon antageligvis vil passe godt.