Stolpediagram
Hva er et stolpediagram? Når bruker vi stolpediagram?
Stolpediagram (også kalt søylediagram) i likhet med søylediagram passer til data med få svaralternativer.
Et stolpediagram har en vannrett akse, en loddrett akse og rektangler (stolper). Et rektangel hører til et svaralternativ. Alle rektanglene er like brede rektangler og avstanden mellom dem er like stor. Høyden til rektanglene er bestemt av antallet i frekvenstabellen.
Stolpediagram kan tegnes enten for hånd eller ved hjelp av et dataprogram, for eksempel Excel. I eksemplet under har vi brukt Excel.
Antall søsken
Elevene i klasse A og B ble spurt om hvor mange søsken de har, og resultatene vises i frekvenstabellen nedenfor.
| Antall søsken | Antall |
| 0 | 6 |
| 1 | 21 |
| 2 | 15 |
| 3 | 3 |
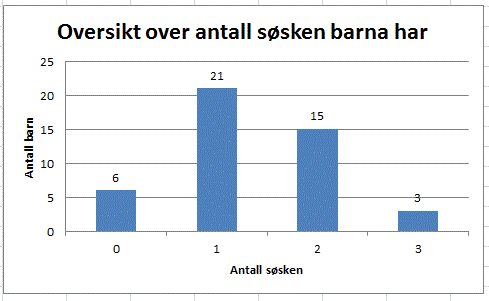
Vi bruker frekvenstabellen og lager et stolpediagram. Til vanlig skriver ikke over rektanglene antallet, men her gjorde vi det slik at du ser at det stemmer overens med frekvenstabellen.
Vi leser raskt ut av stolpediagrammet at de fleste elevene har en eller to søsken. Det er bare tre elever i klassen med tre søsken.
Legg merk til at vi har "snudd frekvenstabellen" slik at den loddrette aksen (y-aksen) viser antallet i hver gruppe på den vannrette aksen (x-aksen).
Del på Facebook
Begrep
-
Ikke-numeriske data
Data som ikke er tall, for eksempel bokstaver, farger og gjenstander.
-
Numeriske data
En datamengde som består av tall.
-
Rektangel
Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:Omkrets:
-
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1. -
Stolpediagram
Et søylediagram uten bredde på søylene.
Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak.
Se Søylediagram