Pavnutij Tsjebysjev

FØDT: 1821

DØD: 1894

Tsjebysjev var professor ved universitetet i St. Petersburg, og kjent for epokegjørende arbeid om primtall som inkluderer bestemmelsen av antallet primtall som ikke er større enn et gitt tall. Han jobbbet også med sannsynlighetsregning og teorien for tilnærminger av algebraiske likninger.

Allerede i tyveårsalderen generaliserte Tsjebysjev Newton-Raphsons metode for numerisk beregning av reelle røtter til likninger, og han fattet interesse for analytisk tallteori da han redigerte Eulers tallteoretiske arbeider.

Hans arbeid med primtall er epokegjørende og inkluderer bestemmelsen av antallet primtall som ikke er større enn et gitt tall. Han skrev en viktig bok, "Teoria sravneny," om kongruensteori i 1849, og i 1850 beviste han antagelsen om at det alltid er minst ett primtall mellom n og 2n.

Han har også satt spor etter seg innen sannsynlighetsregning, og innen teorien for tilnærminger av algebraiske likninger. Han gikk ut fra Taylors resultat om lokal tilnærming av en funksjon og undersøkte uniform tilnærming i et intervall. Han forsøkte, gitt en reell funksjon (x), å finne et polynom P_n(x), slik at maksimum av | (x) - P_n(x) | er minst mulig i det aktuelle intervallet.

I sitt arbeid med integraler generaliserte han den såkalte betafunksjonen og undersøkte integraler på formen

∫ x ^p ( 1 x ) ^q dx.

Tsjebysjev grunnla den matematiske skolen i St. Petersburg, som senere kom til å fostre et stort antall russiske matematikere.

Del på Facebook

Del på Facebook

Skrevet av

Heidi Raude

Institusjon

Universitetet i Oslo

Begrep

Algebraisk ligning

En ligning hvor begge sider av likhetstegnet består av algebraiske uttrykk.

For eksempel: 3 + x = 5x + y
Analytisk tallteori

En gren av tallteorien som tar for seg fordelingen av primtall, tallteoretiske funksjoner og algebraiske og transcendente tall.
Integralregning

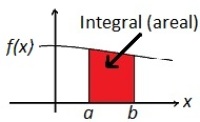
Integralregning er forbundet med arealbegrepet. Et areal kan uttrykkes ved et bestemt integral, og det kan beregnes ved integrasjon. Integralet fra a til b av funksjonen f kan tolkes som arealet av det området som begrenses av funksjonens graf, x-aksen og de vertikale linjene x=a og x=b.
Kongruens

Brukes både i algebra og i geometri.

I geometri: om figurer, for eksempel trekanter, som har parvis like vinkler og sider.

I algebra: om tall, for eksempel i regning modulo, et tall k om to tall som har samme rest etter divisjon med k.
Newton-Raphsons metode

Rekursiv metode der en gjennom suksessive approksimasjoner løser en likning på formen $f (x) = 0$ .

Først bestemmes et startpunkt $x_{0}$ . Tangenten til grafen i punktet $(x_{0}, f (x_{0}))$ skjærer x-aksen punktet $x_{1}$ som vi finner ved å bruke formelen $x_{1} = x_{0} - \frac{f (x_{0})}{f^{'} (x_{0})}$ . Prosessen gjentas ved å bruke $x_{1}$ som startpunkt. Generelt bestemmes $x_{n + 1}$ fra $x_{n}$ etter formelen $x_{n + 1} = x_{n} - \frac{f (x_{n})}{{f^{'} (x}_{n})}$ .

$x_{0}, x_{1}, x_{2}, ....$ konvergerer mot en rot i likningen $f (x) = 0$ . Når prosessen avbrytes, får vi en tilnærmingsverdi.
Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .
Primtall

Positive hele tall større enn 1, som kun er delelig med 1 og seg selv.

Ti fem første primtallene er: 2, 3, 5, 7, 11.
Sannsynlighetsteori

Undersøkelser av mulige utfall av gitte begivenheter sammen med deres relative sannsyligheter og forekomster. Det er faktisk betydelig uenighet omkring nøyaktig hva sannsynlighet betyr i praksis. Noen matematikere anser det bare som en komponent i en abstrakt teori, mens andre gir det en tolkning basert på frekvensen av visse utfall.