Det gylne snitt

Man regner med at det var pytagoreerne som var de første til å studere "Det gylne snitt", og at det er dette arbeidet som ligger bak nedtegnelsene om det gylne snitt i Euclids "Elementer" der det opptrer for første gang. De gamle grekerne baserte seg på geometri og regnet ikke med symboler slik vi gjør i dag, men med lengder. Enkelte forhold og proporsjoner mellom lengder ble sett på som penere enn andre, og det gylne snitt var ett av dem (π var et annet): Ta et linjestykke mellom to punkter A og B og la AB være lengden av linjestykket. Merk av et punkt C mellom A og B slik at forholdet mellom AB og AC er lik forholdet mellom AC og CB, dvs.: $\frac{AB}{AC}=\frac{AC}{CB}$, se figur 1.

Figur 1: Linjestykket som er delt etter forholdet "Det gylne snitt".

Da sier vi at linjestykket er delt etter forholdet det gylne snitt.

Dette forholdet dukket opp i mange av grekernes geometriske konstruksjoner. Etter hvert dukket det også opp i algebraiske sammenhenger og ble assosiert med et tall. Det gylne snitt er tilnærmet lik 1,618. I artikkelen om fibonaccitallene kan du se hvordan man finner den nøyaktige verdien ved å løse en annengradslikning, og også se hvordan denne ligningen brukes til å se sammenhengen mellom fibonaccitallene og det gylne snitt.

Navnet "Det gylne snitt" kommer fra tanken om at man i dette forholdet ville se normen for en fullkommen harmoni i proporsjonene. Det er blant annet brukt innenfor arkitektur, kunst og moteverdenen. Det gylne rektangelet er for eksempel rektangelet der forholdet mellom sidene er det gylne snitt, og dette er pent å se på. Formen på kredittkort er tilnærmet det gylne rektangelet...

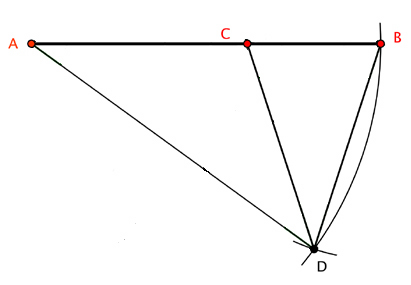
La oss se hvordan vi kan konstruere en regulær 5-kant ved å starte med en linje som er delt opp etter det gylne snitt: La linjestykket AB være delt opp etter det gylne snitt ved punktet C som i tegningen over. Vi bruker en passer og slår en sirkelbue med sentrum i A og radius AB og merker av punktet D på buen slik at AC = BD = CD, se figur 2.

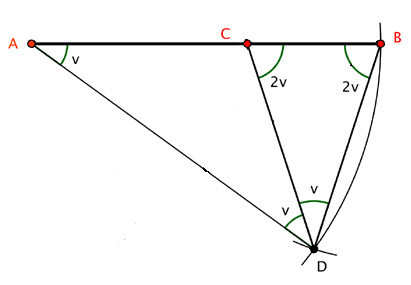
Figur 2: Starten på en regulær 5-kant.

Hvis vi kaller vinkel A for v, blir vinkel BCD lik 2v siden summen av vinklene i en trekant er 180º og en halvsirkelbue er 180º. Trekant ABD er likebeint, og det gylne snitt gir at $\frac{AB}{CD}=\frac{BD}{CB}$. Dermed får vi at trekantene BCD og ABD er formlike, det vil si at trekant BCD er likebeint, og dermed er vinkel B også 2v. Dermed blir vinkel BDC lik v siden trekant ABD er likebeint, slik som i figur 3.

Figur 3: Vinklene i trekantene.

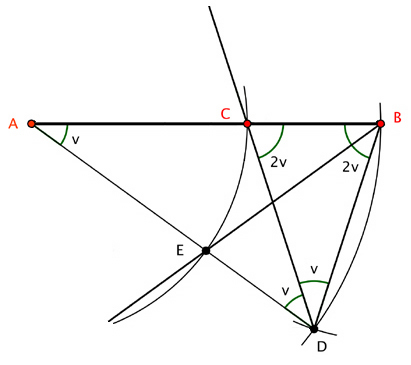
Nå slår vi en sirkelbue med sentrum i A og radius AC, og lar E være skjæringspunktet mellom buen og AD. Da vil E dele AD etter det gylne snitt. Så trekker vi forlengelsene av linjene DC og BE som i figur 4.

Figur 4.

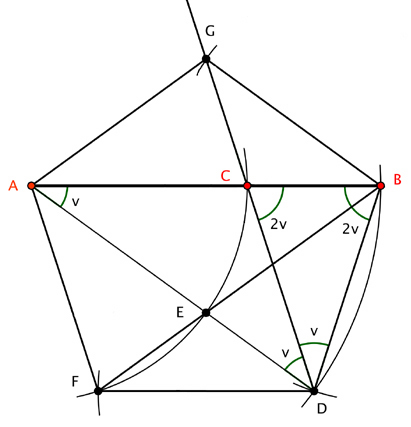
Til slutt setter vi av punktene F og G på disse forlengede linjene slik at BD = DF = BG og trekker linjer.

Figur 5.

Ved å se på trekantene vi får i figur 5, ser vi at AGBDF blir en regulær 5-kant.