Euklid av Alexandria

Euklid av Alexandria
Euklid av Alexandria er den mest prominente matematikeren fra antikken, og er mest kjent for sin framstilling av matematikken i Elementene. Disse bøkene er blitt brukt som lærebøker i geometri helt fram til 1800-tallet.
Euklid av Alexandria er den mest prominente matematikeren fra antikken, og er mest kjent for sin framstilling av matematikken i Elementene. Disse bøkene er blitt brukt som lærebøker i geometri helt fram til 1800-tallet, så Euklid kan trygt kalles den ledende matematikklæreren gjennom tidene. Lite er kjent om Euklids liv utenom at han underviste i Alexandria i Egypt.
"Elementene" er delt i 13 bøker og starter med definisjoner og fem postulater. Bok en til seks tar for seg plan geometri, som trekanter, parallellogrammer og sirkler. Bok syv til ni ser på tallteori. Euklids algoritme for å finne største felles divisor mellom to tall fins for eksempel i bok syv. Bok ti ser på teorien rundt irrasjonale tall, mens bok elleve til tretten ser på tre-dimensjonal geometri. I den siste boka diskuterer Euklid egenskapene til de fem regulære polyedre, og gir et bevis for at det er akkurat fem. Euklids "Elementene" er bemerkelsesverdig for sin klarhet i måten teoremene blir formulert og bevist. Den rigorøse standarden har vært et mål for matematikere siden.
Det er gitt ut mer enn 1000 utgaver av "Elementene" siden den først ble trykket i 1482.
Del på Facebook
Begrep
-
Algoritme
En oppskrift eller en metode med mange steg, som kan brukes for å løse et bestemt type problem.
Vanlige algoritmer er reglene for de fire regningsartene, og oppskriften som brukes for å beregne kvadratrota av et tall.
-
Geometri
Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.
-
Irrasjonale tall
Et reellt tall som ikke kan skrives som en brøk satt sammen av to heltall.
Eksempel: ,
-
Parallellogram
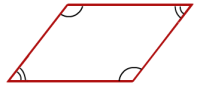
Et parallellogram er en firkant med parvis parallelle sider. Vinklene er parvis like store.
-
Plangeometri
Studiet av geometriske figurer i planet. I den analytiske plangeometrien studeres plane figurer ved bruk av koordinatsystem og algebraiske metoder. Læren om kjeglesnitt er et viktig emne innenfor plangeometri.
-
Regulære polyedre

Polyedre der alle sideflatene er like og alle vinklene er like store. Kalles også Platonske legemer. Det finnes nøyaktig fem forskjellige: Tetraeder, heksaeder (kube), oktaeder, dodekaeder og ikosaeder.






