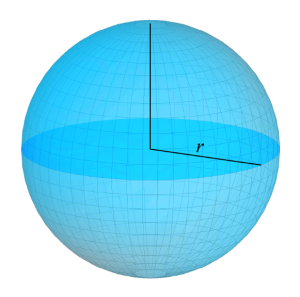
Å sette inn i formelen

Når vi har formelen klar, så er det viktigste å bruke den riktig. Etter hver gang en formel er blitt brukt, er det viktig å se nøye på svaret og vurdere om det stemmer for å sjekke at vi har brukt formelen riktig. Vi skal se på hvordan vi bruker formler under.

Golfball

Overflatearealet til golfballen, og formelen er $O=4\pi r^2$. Siden $O$ står alene på venstresiden, så er det naturlig å sette inn en verdi for $r$ og se hva overfaltearealet blir.

 

På en nattturnering i golf skal golfballene kles inn i et selvlysende stoff. Radiusen til en golfball er ca. $2,30$ cm. Hvor mye selvlysende stoff trenger man for å kle inn én ball?

For å vite hvor mye stoff som trengs setter vi $r=2,30$ cm. Da bytter vi bare ut $r$ i formelen med $2,30$ cm.

$O=4\pi (2,30\text{ cm}{)}^2$

$O=66,48{\text{ cm}}^2$

Vi ser da at vi trenger $66,48{\text{ cm}}^2$ med skinn for hver golfball.

Globus

Et firma lager kart som blir limt på globuser. Et av kartene firmaet laget har overflateareal på $15{\text{ m}}^2$. Hva er radiusen til globusen kartet blir limt på?

Vi skriver formelen om slik at vi får $r=\frac{\sqrt{O}}{2\sqrt{\pi }}$.

Hva må radiusen være dersom $O=15{\text{ m}}^2$. Vi bytter igjen ut $O$ med $15{\text{m}}^2$ og regner ut.

$r=\frac{\sqrt{15{\text{ m}}^2}}{2\sqrt{\pi }}\approx 1,1\text{ m}$

Globusen vil ha en radius på ca. $1,1\text{ m}$.