Gjøre om formlene
Så lenge vi kjenner til en av vei, fart og tid-formlene, kan vi finne de andre formlene ved å skrive om den vi kjenner. La oss si at vi kjenner til , og vil finne de andre formlene. Først finner vi formelen for strekning:
Vi finner deretter formelen for tid:
Da har vi funnet de to andre formlene for vei, fart og tid ut ifra bare en av dem. Nå kan vi se på noen eksempler på hvordan vi kan bruke disse formlene.
Marte
Marte bor meter unna skolen. Det tar henne minutter å gå hjem, og hun mener da at hun går med en fart på meter i sekundet.
For å sjekke farten bruker vi at farten er lik strekingen dividert på tiden, . Vi må ta strekningen, meter, og dividere med tiden som er i sekunder, altså sekunder. Dette gjøres slik;
Så Marte går ikke med en fart på , men heller med en fart på .
Ahmed
Ahmed blir alltid henta i parken av faren sin, som kjører i kilometer i timen hele veien. De er hjemme etter minutter. Ahmed mener derfor at han bor kilometer unna.
For å sjekke strekningen bruker vi at strekningen er lik farten multiplisert med tiden, . Vi må ta strekningen, kilometer, og multiplisere med tiden i timer, altså time.
Ahmed har rett, han bor kilometer unna parken.
Silje
Det er en løype man kan løpe i parken. Den er én kilometer lang, og Silje satser alltid på å holde en fart på meter i sekundet. Silje føler at bruker rett under tre minutter og sekunder på å løpe løypen.
For å sjekke tiden, bruker vi at tiden er lik strekningen dividert på farten, . Vi må ta strekningen i meter, altså meter, og dividere med farten, .
sekunder er tre minutter og sekunder. Silje har rett, hun løper løypa på rett under tre minutter og sekunder.
Del på Facebook
Begrep
-
Brøk
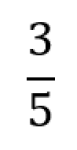
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.




