En andregradslikning med absoluttverdi

Vi vil løse likningen

| x^{2} - 8 x + 7 | = 9.

Vi blir kvitt absoluttverditegnet ved å splitte opp likningen og ta vare på de ulike fortegnene. Likningen i dette eksempelet kan deles opp i likningene

x^{2} - 8 x + 7 = 9

eller

- (x^{2} - 8 x + 7) = 9.

som gir to

Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.

andregradslikninger

. Det betyr at vi kan få høyst fire løsninger (to fra hver av likningene). Den første likningen gir

x^{2} - 8 x - 2 = 0

med løsninger

x = \frac{8 \pm \sqrt{64 + 8}}{2} = \frac{8 \pm \sqrt{72}}{2} = \frac{8 \pm 6 \sqrt{2}}{2} = 4 \pm 3 \sqrt{2} .

Den andre likningen gir

x^{2} - 8 x + 16 = 0,

og ved hjelp av

Andre kvadratsetning

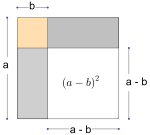
Andre kvadratsetning sier at

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ .

andre kvadratsetning

ser vi at dette er

{(x - 4)}^{2} = 0

(kvadratsetningene kan du repetere i lynkurset om andregradsuttrykk). Da har denne likningen én løsning:

x = 4

Vi vet da at de tallene $x$ som gir $| x^{2} - 8 x + 7 | = 9$ er $x = 4 \pm 3 \sqrt{2}$ eller $x$ = 4.

Likningen vår har altså tre løsninger.

Del på Facebook

Del på Facebook

Lynkurs 11.-13.trinn

Absoluttverdi

Består av:

Likningen Ix+1I=6
Likningen Ix+1I = Ix-1I
En andregradslikning med absoluttverdi

Begrep

Absoluttverdi

Absoluttverdien til et tall er avstanden fra null og ut til tallet, på tallinjen. Absoluttverdien til tallet 5 er 5 og skrives slik $| 5 | = 5$ ,
absoluttverdien til –5 er også 5 og skrives slik $| - 5 | = 5$ .

Absoluttverdien til et reelt tall x defineres slik:
$| x |$ = {x hvis x > 0, -x hvis x < 0}
Andregradslikning

En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:

$a x^{2} + b x + c = 0$

Likningen kan løses ved hjelp av abc-formelen.