Ordliste
Her finner du en liste over matematiske begreper med korte forklaringer.
Tallteori
Abakus
Kuleramme eller brett for å utføre regneoperasjoner. Den vanligste formen av abakus er en ramme utstyrt med pinner der det er kuler som kan beveges fritt. Abakus kalles ofte for kuleramme.
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
Abelsk gruppe
En gruppe hvor tilordningsregelen er kommutativ, altså hvor a × b = b × a.
Abelske funksjoner
En Abelsk eller hyperelliptiske funksjon er en spesiell type løsning på en abelsk ligning og blir definert ved inversjon av et abelsk integral. Abelske funksjoner har fått navn etter den norske matematikeren Niels Henrik Abel.
Absoluttverdi
Absoluttverdien til et tall er avstanden fra null og ut til tallet, på tallinjen. Absoluttverdien til tallet 5 er 5 og skrives slik ,
absoluttverdien til –5 er også 5 og skrives slik .
Absoluttverdien til et reelt tall x defineres slik:
= {x hvis x > 0, -x hvis x < 0}
Abstrahere
Å trekke frem viktige egenskaper ved noe, og se bort fra de uviktige.
Eksempel: En strekfigur er en abstrahering av et menneske.
Addisjon
Er det samme som å legge til, legge sammen eller plusse sammen.
Regneoperasjonen 5 + 7 = 12 kalles en addisjon.
Tallene 5 og 7 kalles ledd, og resultatet, 12, kalles en sum.
Mellom leddene skrives plusstegn +.
Addisjonssetningen
Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Akselerasjonsvektor
Akselerasjon betegnes med en vektor, gjerne , siden akselerasjon har en retning.
Algebra
Algebra er den delen av matematikken som handler om strukturer, relasjoner og kvantiteter. I skolen er algebra ofte brukt som betegnelse på regning med bokstavuttrykk og ligninger.
Et algebrauttrykk kan være:
n + n + n + n + n = 5n
Her har vi lagt sammen n til sammen 5 ganger.
Algebraisk ligning
En ligning hvor begge sider av likhetstegnet består av algebraiske uttrykk.
For eksempel: 3 + x = 5x + y
Algebraisk løsning
Løsning ved regning, i motsetning til for eksempel grafisk løsning.
Algebraiske tall
Tall som kan være løsning til en algebraisk ligning med heltall som koeffisienter. Tallet er et eksempel på et algebraisk tall, ettersom det er løsning til ligningen .
Algebraiske tallkropper
Delmenger av de komplekse tall som inneholder alle rasjonale tall, og som er endelige kroppsutvidelser av de rasjonale tallene.
Algoritme
Algoritme
En oppskrift eller en metode med mange steg, som kan brukes for å løse et bestemt type problem.
Vanlige algoritmer er reglene for de fire regningsartene, og oppskriften som brukes for å beregne kvadratrota av et tall.
Algoritmisk tenkning
Algoritmisk tenkning betyr at man splitter et stort problem opp i mindre deler. Man sorterer informasjonen man har på en logisk måte, og lager algoritmer (løsningsmetoder) for hvordan man kan løse problemet. Denne tenkemåten brukes blant annet i programmering.
Analyse
Den matematiske analyse studerer ulike fenomeners forandringsprosesser eller dynamikk, og gjør blant annet bruk av grenseverdi og kontinuitet. Eksempler på deler av analysen er funksjoner av en eller flere reelle variabler, funksjoner av komplekse variabler og trigonometriske rekker.
Analysens fundamentalteorem
Analysens fundamentalteorem beskriver hvordan integrasjon er det samme som antiderivasjon.
Teoremet sier at dersom f er en kontinuerlig funksjon i intervallet [a,b] og F = der x er i intervallet [a,b] så er F'(x) = f(x), F er altså den antideriverte til f. Vi bruker blant annet teoremet til å regne ut integraler på følgende måte: = F(b) - F(a) Eksempel: = , her har vi brukt at den antideriverte til er fordiAnalytisk geometri
Den delen av geometrien hvor man undersøker geometriske egenskaper ved å bruke koordinater. En ligning i to variable x og y, har løsninger som en kan finne igjen som en punktmengde i et koordinatsystem med en x-akse og en y-akse. Linjer og kjeglesnitt er løsningsmengder til hhv. første- og andregradslikninger.
Analytisk tallteori
En gren av tallteorien som tar for seg fordelingen av primtall, tallteoretiske funksjoner og algebraiske og transcendente tall.
Anbud
Anbud er et bindende tilbud om å levere en tjeneste, gjøre et arbeid eller levere varer. Den som ønsker arbeidet utført eller tjenesten levert, bestemmer betingelsene.
Eksempel: Du ønsker å male huset ditt, og legger ut et anbud på Finn.no, der du skriver at du vil få huset malt så fort som mulig, og så billig som mulig. Deretter kan malerfirmaene kontakte deg og gi sine pristilbud, og forklare når de kan utføre jobben.
Andre koordinat
Andre koordinat er et punkts verdi langs andreaksen i koordinatsystemet.
Når et punkt beskrives med et tallpar (5,3), er andrekoordinaten det andre tallet i tallparet, 3 i dette eksempelet.

Andre kvadratsetning
Andre kvadratsetning sier at
.
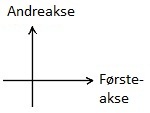
Andreakse
Den vertikale/loddrette aksen i et koordinatsystem. Kalles også y-aksen.
Andrederivert
Når vi deriverer en funksjon fto ganger, finner vi den andrederiverte ƒ′′. Vi har ƒ′′= (ƒ′)′. For eksempel hvis ƒ(x) = x2, så er ƒ′(x) = 2x og ƒ′′(x) = 2.
Andrederiverte
Den andrederiverte til en funksjon er funksjonen derivert to ganger og skrives eller . Kalles også annenderiverte eller dobbeltderiverte.
Andregradslikning
En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:
Likningen kan løses ved hjelp av abc-formelen.
Andregradsulikheter
En andregradsulikhet er en ulikhet der den ukjente er i andre grad. Ulikhetene kan løses grafisk eller ved å bruke fortegnsskjema.
Eksempler:
Andregradsuttrykk
Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.
Annuitetslån
Annuitetslån er et lån som betales tilbake i like store beløp hver termin. Beløpet som belastes består av avdrag og renter.
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Arealenheter
Mål for areal:
km², m², dm², cm², mm²
Andre mål:
1 ar = 100 m2
1 dekar = 10 ar = 1000 m2 = 1 mål
(deka betyr 10)
Omgjøring mellom enheter:
1 m² = 1 m · 1 m = 10 dm · 10 dm = 100 dm²
1 dm² = 1 dm · 1 dm = 10 cm · 10 cm = 100 cm²
1 cm² = 1 cm · 1 cm = 10 mm · 10 mm = 100 mm²
Arealsetningen
For en trekant er arealet gitt ved .
Argumentasjon
Når man argumenterer viser man sin egen tankegang for å styrke eller svekke en påstand, gjerne for å overbevise andre i en diskusjon. I matematikken betyr dette at man må begrunne påstandene sine og forklare fremgangsmåten man bruker.
Eksempel på argument: er større enn , fordi fellesnevneren til brøkene er 20, og .
Aritmetikk
Vanlig regning med hele tall. Omfatter de fire regningsartene, brøkregning, potensregning og rotutdragning.
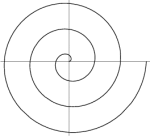
Arkimedes' spiral
Spiralkurven er grafen til funksjonen (i polarkoordinater) r =v , der r er avstand til sentrum, og v er vinkelen mellom posisjonsvektor og positiv x-akse. Funksjonen kan også skrives som (kartesiske koordinater).
Assosiativ lov
Gjelder for addisjon og multiplikasjon. For addisjon med tre tall :
Det vil si at vi får samme svar om vi først regner ut og så legger til , eller om vi først regner ut og legger til .
For multiplikasjon:
Avdrag
Avdrag er delvis betaling av gjeld, det vil si en sum som betales som en del av en større totalsum.
Avrunding
Avrunding brukes når vi klarer oss med en tallverdi som ikke er helt nøyaktig.
Avrundingstegnet, ≈, bruker vi slik:
658 ≈ 700
Og vi leser det: 658 er tilnærmet lik 700.
Det er regler for hvordan vi skal runde av et tall.
Avstand
Mål for hvor langt geometriske objekter ligger fra hverandre. For eksempel avstanden mellom to punkter.

Balanse og likevekt
Dersom noe er i likevekt, er det like mye på hver side.
Eksempler:
Her har vi like mye på venstre og høyre side av likhetstegnet. Dette gjelder alltid når man bruker likhetstegn.
På figuren ser vi en skålvekt. Denne er i balanse når det er like mye vekt på hver side.
Bayes' setning
Bayes' setning sier at
Begivenhet
En begivenhet er en delmengde av utfallsrommet og består av ett eller flere utfall.
· Å få 6 på en terning er et eksempel på en begivenhet, der utfallsrommet består av 1, 2, 3, 4, 5 og 6. Å få høyere enn 3, altså 4, 5 eller 6, er et annet eksempel på en begivenhet.
Benevning
En bokstavkode som står etter måltallet. Eksempelvis forteller 25,2 kg, at vi har med masse å gjøre. Benevningen kg er en forkortelse for kilogram. Måltallet (25,2) forteller oss noe om mengden.
Eksempel på andre benevninger:
g, dL, h, km/h, g/cm3
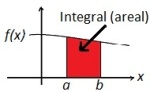
Bestemt integral
Integralet av en funksjon mellom to grenser.
For en reell kontinuerlig funksjon med positive funksjonsverdier, kan det bestemte integralet tolkes som arealet av området begrenset av grafen til funksjonen, x-aksen og de to grenseverdiene.
Det skrives
a og b er grenseverdiene, og f(x) er funksjonen vi integrerer.
Betinget sannsynlighet
Den betingede sannsynligheten er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.
.
Binomialkoeffisient
Binomialkoeffisienten
hvor ,
forteller hvor mange måter det kan trekkes m objekter ut fra en samling av n gjenstander uten tilbakelegging.
Binomialkoeffisienter
De koeffisientene man får når en opphøyer (x+y) i et naturlig tall.
Binomisk fordeling
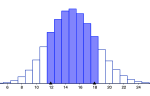
Binomisk fordeling er en sannsynlighetsfordeling som forteller hvor mange ganger en bestemt hendelse inntreffer i løpet av et bestemt antall uavhengige forsøk.
Formelen beskriver sannsynligheten for at en hendelse inntreffer ganger av totalt forsøk, dersom sannsynligheten for at hendelsen inntreffer er . Figuren viser en binomisk fordeling der og .
Eksempel: Hva er sannsynligheten for at vi får tre femmere på ti terningkast? Her er siden det er sannsynligheten for å få én femmer på ett kast, og fordi vi kaster ti ganger. fordi vi ser på sannsynligheten for å få tre femmere.
Setter vi dette inn i formelen får vi at:
Binomisk forsøk
Et binomisk forsøk må tilfredsstille følgende krav:
- Antall delforsøk n er fast.
- Alle delforsøkene er uavhengige.
- For hvert delforsøk er det kun to mulige utfall. Det utfallet vi er interessert i kalles for suksess, mens det andre er kalt for fiasko.
- For hvert delforsøk er sannsynligheten for suksess lik p.
Blanda tall
Et tall som består av en heltallsdel og en brøkdel.
Et eksempel er: som betyr .
Vi utelater plusstegnet for å få en enklere skrivemåte.
Boolsk algebra
Brukes for å beskrive funksjoner i digitale kretser og er algebra med variabler som kun kan ha to verdier: SANN/USANN.
Brudden brøk
En brudden brøk har en brøk i teller eller nevner, eller i begge.
Eksempel:
Brutto månedslønn
Det beløpet du mottar fra arbeidsgiver i måneden, før skatter og avgifter er trukket fra.
Bruttoinntekt
Bruttoinntekt er inntekten man får fra arbeidsgiver, før man har trukket fra skatt og utgifter.

Brøk
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Budsjett
Budsjett er en oppstilling over forventede inntekter og utgifter over en bestemt periode.
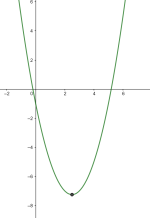
Bunnpunkt
Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Cauchy-Riemann likningen
En likning som de partiell deriverte til en kompleks funksjon må oppfylle for å være deriverbar.
Cellereferanser
Cellereferanser refererer til en celle i et regneark (eller et celleområde).Disse kan vi bruke i en formel for at Microsoft Office Excel kan beregne eller hente ut nyttige verdier for oss. Dette brukes blant annet hvis man skal lage diagrammer eller grafer.
Eksempel: skriv '=B5' i en celle og trykk 'enter', da vil Excel returnere verdien som står i celle B5.

Cosinus
Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Cosinussetningen
La være en trekant. Anta at vi kjenner sidene , og mellom dem. Da er
Data
Opplysninger som vi samler inn kalles data.
Data kan for eksempel være 3, 5, 10, 41 og 41, som er alderen i en familie bestående av fem personer. Data kan også være blå, grønn, gul, som er farger på biler.
Datasett
En organisert samling av data i eksempelvis en tabell eller en liste.
Eksempel: En klasseliste med navn og etternavn til elevene i en skoleklasse.
De Morgans lov
Loven i mengdelære som sier at komplementet til en union av to mengder er lik snittmengden til komplementene til de to mengdene, og at komplementet til snittet av to mengder er lik unionen av komplementene til de to mengdene.
Dedekind snitt
Brukes til å beskive komplettheten til de reelle tall, og sier at hvis alle elementene i en reell delmengde A er mindre enn alle elementene i en reell delmengde B, så fins det et reelt tall som større eller lik alle elementene i A og mindre eller lik alle elementene i B.
Definisjonsmengde
En funksjon tar verdier fra en bestemt mengde, og denne mengden kalles definisjonsmengden til funksjonen.
Eksempel:
har definisjonsmengde . Merk at funksjonen ikke kan være definert i fordi vi ikke kan dele på .
Dekadiske enheter
Tall som bare består av sifferet 1 etterfulgt av nuller, kaller vi dekadiske enheter. 1000 er en dekadisk enhet.
Delbrøksoppspaltning
En metode for å dele/spalte opp rasjonale uttrykk, der graden til telleren er mindre enn graden til nevneren, i flere "enklere" ledd. Brukes blant annet når vi skal antidereivere/integrere slike uttrykk: Ved å delbrøkoppspalte uttrykket kan vi antiderivere ledd for ledd, siden leddene er enklere/mulig å antiderivere.
Delelig
Vi forklarer med et eksempel:
18 : 3 = 6
Denne divisjonen "går opp" - det blir ingen rest, det vil si ingen tall etter komma. Vi sier da at 18 er delelig med 3.
Delingsdivisjon
Delingsdivisjon har vi når en mengde skal deles opp i et bestemt antall deler.
Eksempel: En klasse med 30 elever skal deles i 5 grupper. Hvor mange elever er det på hver gruppe? 6 elever.
Delmengde
En mengde A er en delmengde av mengde B, dersom alle elementene i A også er i B.
Eksempel: , som leses A er delmengde av B, fordi
Delvis integrasjon
En metode for å antiderivere/integrere et uttrykk der vi har et produkt. Vi utnytter produktregelen for derivasjon baklengs. Formelen er u`v dx = uv - v`u dx.
Den deriverte
Når vi sier “den deriverte” mener vi “den deriverte funksjonen til en funksjon”. Når vi deriverer en funksjon f, får vi en ny funksjon ƒ′.For eksempel hvis ƒ(x) = x2, så er ƒ′(x) = 2x, og vi sier at den deriverte til x2 er 2x.
Den pytagoreiske læresetning
Se Pytagoras læresetning
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Derivasjonsregler
Regler som forteller hvordan man kan derivere ulike funksjoner.En praktisk anvendelse er å beregne akselerasjonen fra en fartsfunksjon, siden akselerasjonen er definert som den tidsderiverte av farten.
Eksempler:
f(x) = ln(x) ⇔ f'(x) = 1/x
Deriverbar
En funksjon ƒ er deriverbar i et punkt a hvis grenseverdien eksisterer (dvs. er lik et tall og er det samme uavhengig av om h går mot null ovenfra eller nedenfra). Vi skriver ƒ′(a)for denne grenseverdien.
Deriverbarhet
Vi sier at en funksjon er deriverbar i et punkt , hvis følgende grense finnes:
Med "finnes" mener vi at den ikke er uendelig og blir det samme uavhengig av om h går mot null ovenfra eller nedenfra.
Desimaltall
Desimaltall er tall som inneholder komma.
Eksempel: 2,34 og 18,001
Sifrene som følger etter komma, kalles desimaler.
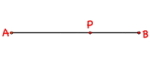
Det gylne snitt
Det gylne snitt er et forholdstall og en måte å dele et linjestykke på slik at de to delene står i et bestemt forhold til hverandre og til helheten.
Forholdstallet er: .
Når et linjestykke er delt etter , er linjestykket delt etter forholdet til det gylne snitt.
Denne delingen av linjestykket har hatt stor betydning i kunst og arkitektur, da det skal være behagelig for øyet.

Diagonal
Linjestykke som forbinder to ikke nærliggende hjørner i en mangekant.
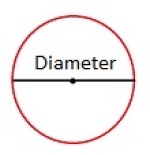
Diameter
En rett linje som forbinder to punkter på sirkelbuen og som samtidig går gjennom sentrum.
Lengden av en diameter, d, er lik to radier, r. d=2r.
Differanse (mengder)
Differansen mellom mengden A og mengden B betegnes med og er mengden av alle elementer som er i B men ikke i A.
Differanse (tall)
Utrykket a − b kalles differansen mellom a og b.
10 − 2 = 8. Differansen mellom 10 og 2 er 8.
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
Dimensjon
Geometrisk er det lik det minste antall koordinater som er nødvendig for å representere et punkt i et rom. For eksempel har en linje dimensjon én, et plan dimensjon to, og det vanlige rommet har dimensjon tre.
Se også todimensjonal og tredimensjonal.
Disjunkte hendelser
A og B kalles disjunkte dersom de ikke har noen felles elementer. Dette betyr at , altså at det ikke er noen elementer som er både i A og i B.
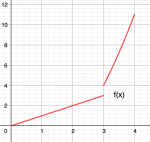
Diskontinuerlig funksjon
En diskontinuerlig funksjon er en funksjon som har ett eller flere punkt der den ikke er kontinuerlig. For at en funksjon f skal være kontinuerlig for x = b må
Dette betyr at grenseverdien må være den samme enten vi nærmer oss x = b fra høyre eller fra venstre.
Eksempel: På figuren kan vi se at når vi nærmer oss x = 3 fra venstre, men når vi nærmer oss x = 3 fra høyre. Siden grenseverdiene er ulike betyr dette at funksjonen f er diskontinuerlig for x = 3.
Diskriminant
For en andregradslikning kalles tallet for diskriminanten. Om dette tallet er negativt har likningen ingen løsninger, om det er 0 har den én, og om det er positivt har likningen to løsninger.
Dividend
Dividenden er det første tallet i en divisjon. Dividenden forteller hvor mye vi har før vi begynner å dele.
I eksemplet: 32 : 8 = 4, er 32 dividenden.
Divisjon
Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.
Eksempel: fordi .
Divisjonstegn
Regnetegnet for divisjon er enten : eller / (brøkstrek).
Divisor
Divisor er det andre tallet i en divisjon.
Eksempel: 32 : 8 = 4. Her er 8 divisoren.
Når divisjonen skrives som brøk, kalles divisoren nevner.
Doble
Doble betyr å legge til like mye som en allerede har. Det er det samme som å multiplisere med 2.
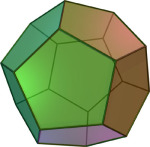
Dodekaeder
Et legeme begrenset av 12 kongruente, regulære femkanter.
Et dodekaeder er ett av de fem platonske legemer.
Dreining
Se rotasjon.
e
Det er et irrasjonalt tall med uendelig mange desimaler.
e = 2,718281828...
Tallet er grunntallet for den naturlige logaritmen og ble introdusert av Euler som har fått tallet oppkalt etter seg.
Tallet kan defineres som når n går mot uendelig.
Egenskaper til to- og tredimensjonale figurer
I matematikken kan vi måle og regne ut egenskaper til mange figurer. Det kan være todimensjonale figurer som sirkler, kvadrat og rektangler, eller tredimensjonale figurer som kuler, prismer eller pyramider.
Eksempler på egenskaper: areal, volum, omkrets, vinkelsum
Eksakte verdier for sinus, cosinus og tangens
|
ikke def. |
Eksplisitt formel
En eksplisitt formel gir verdien til et ledd i en tallfølge dersom vi kjenner leddnummeret .
Eksempel:
Vi finner ledd nummer fem:
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
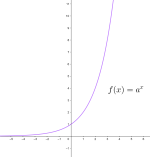
Eksponentialfunksjon
En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Eksponentialligning
En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.
Eksempel med som ukjent: eller

Eksponentiell vekst
Dersom veksten er proporsjonal med størrelsen selv, har man eksponentiell vekst. Man kan også si at det er konstant prosentvis endring. I figuren ser du hvordan eksponentiell vekst kan se ut.
Eksempler på eksponentielle funksjoner: ,
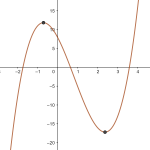
Ekstremalpunkt
Vi sier at et punkt er et ekstremalpunkt for en funksjon hvis det enten er et toppunkt eller bunnpunkt for funksjonen.
Ekte brøk
En brøk der telleren har mindre verdi enn nevneren.
Eksempel:
Ekvivalens
Man sier at to påstander og er ekvivalente hvis følgende er sant:
1) Hvis er sann, må også være sann.
2) Hvis er sann, må også være sann.
Vi skriver , som leses er ekvivalent med .
Eksempel: "Hvis Ida er i Frankrike, er hun i Europa" er ekvivalent med "hvis Ida ikke er i Europa, er hun ikke i Frankrike".
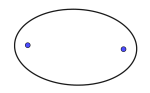
Ellipse
Et kjeglesnitt med eksentrisitet e mellom 0 og 1.
Kan også defineres ved at summen av de to brennpunktradiene til et vilkårlig punkt P alltid er en konstant. En sirkel er et spesialtilfelle av en ellipse, med sammenfallende brennpunkter.
Elliptiske funksjoner
Dobbeltperiodiske komplekse funksjoner. Pioneren i studiet av disse funksjonene var Niels Henrik Abel som definerte disse som omvendte funksjoner til elliptiske integraler.
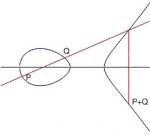
Elliptiske kurver
En algebraisk kurve gitt av en tredjegradslikning i to variable. Punktene på en elliptisk kurve danner en gruppe. Niels Henrik Abel studerte denne gruppa ved hjelp av elliptiske integraler og elliptiske funksjoner.
En-til-en-korrespondanse
Det betyr at hvert element i en mengde har nøyaktighet ett tilhørende element i en annen mengde, og omvendt.
Dette er viktig for opptelling av objekter, der hvert objekt må kobles til ett tallord.
Endelige mengder
En mengde som har et endelig antall elementer, og det må i prinippet være mulig å telle antall elementer.
Eksempler: Mengden av barn i en klasse eller mengden av alle sandkorn på jorda. Mengden av naturlige tall er derimot ikke endelig.
Enere
Sifferet som står på enerplassen forteller hvor mange enere det er i tallet.
Eksempel: tallet 286 har 6 enere.
Enerplass
I et helt tall, for eksempel 3185, er enerplassen lengst til høyre. Her står sifferet 5 på enerplassen.
Ensifra tall
Med siffer mener vi det skrifttegnet vi bruker for å skrive et tall. Ensifra tall skrives med bare ett siffer.
De ensifra tallene er: 0, 1, 2, 3, 4, 5, 6, 7, 8 og 9.

Episykloide
Den plane kurven et fast punkt på en sirkel beskriver når sirkelen ruller langs ytterkanten av en fast sirkel.
Fagtekst
En fagtekst er en faktabasert tekst som handler om noe virkelig.
Eksempler på fagtekster: tekstene i et leksikon, en lærebok i matematikk
Faktor
I en multiplikasjon kalles tallene faktorer. Resultatet kalles et produkt.
Eksempel: 5 · 3 = 15. Her er 5 og 3 er faktorer. Tallet 15 er produktet. Vi kan si at 15 består av faktorene 5 og 3.
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
Faktorisering av uttrykk
Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.
Eksempel:
Fart
Fart er tilbakelagt distanse per tidsenhet.
Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.
Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.
Felles faktor
En felles faktor er et tall som finnes som faktor i to eller flere tall. Største felles faktor er det største tallet som er felles faktor.
Eksempel: 12 og 8, her er 2 og 4 felles faktor og 4 er den største felles faktor.
Felles multiplum
Et felles multiplum for to tall a og b, er et tall som a og b er en faktor i.
Minste felles multiplum (mfm) er viktig i brøkregning. Det er det minste tallet som er et felles multiplum for a og b.
Eksempel: for tallene 20 og 25, er for eksempel 100 og 200 felles multiplum. Minste felles multiplum er 100 og kan skrives: mfm(20, 25) = 100.
Fellesnevner
Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.
Eksempel: , 42 er fellesnevner for disse to brøkene.
Femkant
Femkant er en geometrisk figur med fem sidekanter.
Fermats siste setning
Følgende berømte antagelse: Likningen xn + yn = n har ingen heltallsløsninger når n > 2 og x, y og z alle er ulik 0.
Fibonacci-tallene
Tallfølgen 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,... kalles Fibonacci-tallene. Det neste tallet i følgen finner vi ved å ta summen av de to foregående tallene. Det neste tallet er 34 + 55 = 89.
Fibonacci-tallene forekommer ofte i naturen, for eksempel i forbindelse med spiraler i kongler og solsikker.

Figurmønster
Når man gjør om en tallrekke til et geometrisk mønster, får man et figurmønster. Det er en bestemt sammenheng mellom antall elementer i figurene og figurnummeret.
Eksempel: på figuren ser vi figurmønsteret for kvadrattallene. Her er ledd nummer n gitt som . Figur nummer tre er vi ser at dette stemmer med figuren.
Firkant
En firkant er en geometrisk figur med fire hjørner og fire sidekanter.
Flate
I geometri kan en flate beskrives som overflaten til et objekt, for eksempel en terning. En terning har seks sider, det vil si at den har seks sideflater. En flate er en todimensjonal del av rommet. Arealet til en flate er et mål på flaten sin utstrekning.
Flersifrede tall
Med siffer mener vi det skrifttegnet vi bruker for å skrive et tall. Flersifrede tall har to eller flere siffer. Tallene fra 10 og oppover er flersifrede.
Forkorte brøk
En brøk kan omgjøres til en likeverdig brøk ved å dividere med det samme tallet både i telleren og i nevneren. Dette kalles å forkorte brøken.
Eksempel:
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Formler i dagligliv
Dette er formler man bruker i hverdagen.
Eksempel:
Dersom man kjører i 70 km/t i 27 minutter, hvor langt har man kjørt da?
Her har vi gjort om 27 minutter til siden det er 60 minutter i en time.
Formler i yrkesliv
Dette er formler man får bruk for på jobb.
Eksempel: Elektrikeren måler spenningen over en meterlang varmekabel til å være og strømmen gjennom kabelen er , hvor høy er effekten per meter varmekabel?
Ved hjelp av formelen
finner hun at
Så effekten er 16 watt per meter varmekabel.

Formlike trekanter
To trekanter er formlike hvis de har parvis like store vinkler.
Eksempel: , det leses trekant ABC er formlik med trekant DBE.

Formlikhet
Dersom to figurer kan forstørres eller forminskes slik at de blir helt like, er figurene formlike. Forholdet mellom tilsvarende sider i figurene er like, og tilsvarende vinkler er like, dette gjelder alltid for formlike figurer.
Eksempler: Kvadrater er alltid formlike, trekanter med parvis like store vinkler er alltid formlike.
På figuren ser vi at trekant ABC er formlik trekant DEF, som vi skriver , fordi de har parvis like store vinkler

Forsvinningspunkt
Dette er det punktet der to eller flere parallelle linjer som beveger seg bort fra tilskueren ser ut til å møtes.

Fortegnsskjema
Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.
Forventningsverdi
Forventningsverdien er den verdien man forventer å få når man gjennomfører et forsøk.
Matematisk er den gitt ved
Her er X en stokastisk variabel og utfallsrommet er
Sannsynligheten for å få en bestemt verdi er
Eksempel: Vi kaster én terning én gang. Et terningkast er en uniform sannsynlighetsmodell, så
Forventningsverdien ved terningkastet er 3,5. I praksis betyr dette at ved svært mange terningkast, ville gjennomsnittet nærmet seg 3,5.
Fourier-rekker
Uendelige rekker av sinus og cosinus funksjoner som brukes til å beskrive og regne med periodiske funksjoner.
Fraktal
En fraktal er en svært oppstykket kurve eller flate, som er slik at hver liten del har samme form som det hele.
Framstilling av data
Data kan framstilles på mange ulike måter. Avhengig av hva man vil vise, kan man velge ulike framstillinger.
Eksempel: i en tabell, et diagram, en graf, liste
Frekvens
Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer.
Se frekvenstabell

Frekvenstabell
En frekvenstabell er en opptelling og ordning av dataene i en datasamling.
Se frekvens
Fullføre kvadratet
Omskriving av et andregradsuttrykk slik at det likner mest mulig på et fullstendig kvadrat, altså få uttrykket på formen til der er en konstant, kalles å fullføre kvadratet.
Fullstendig kvadrat
Et kvadrat (ofte kalt et fullstendig kvadrat) et et uttrykk som er opphøyd i 2, for eksempel
.
Fundamentalteorem
Et grunnleggende resultat.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi

Første kvadratsetning
Første kvadratsetning sier at
.

Førsteakse
Den horisontale/vannrette aksen i et koordinatsystem. Kalles også for x-akse.
Førstederivert
Når vi deriverer en funksjon f én gang, finner vi den førstederiverte ƒ′.
Førstekoordinat
Førstekoordinat er et punkts verdi langs første-aksen, eller x-aksen i koordinatsystemet. Når et punkt beskrives med et tallpar (7,3), er førstekoordinaten det første tallet i tallparet, 7 i dette eksempelet.
Galois teori
En teori for løsbarhet av n-tegradslikninger i en variabel. Første-, andre-, tredje- og fjerdegradslikningene kan alle løses ved rotutdragning. Abel viste at den generelle femtegradslikningen ikke kan løses ved rotutdragning, mens Galois viste hvilke ligninger som kan løses på den måten.
Generalisere
Se generalisering
Generalisering
Generalisering i matematikk betyr at man kommer frem til sammenhenger og strukturer som gjelder generelt.
Eksempel: Den kommutative loven sier at og dette er en generalisering av et spesialtilfelle som for eksempel
Geometri
Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.

Geometriske mønster
Et mønster er noe som gjentar seg på en forutsigbar måte. Geometriske mønster består av geometriske figurer som blant annet trekanter, kvadrater og sirkler.
Eksempel: Bildet viser et geometrisk mønster.
Gjeldende siffer
Vi definerer antall gjeldene siffer som det totale antall siffer med unntak av eventuelle nuller til venstre.
Eks:
30 000 har fem gjeldende siffer
30,001 har fem gjeldene siffer
0,0001 har ett gjeldende siffer
0,0300 har tre gjeldende siffer
Tall på formen b · 10ª der a er et helt tall og 1 ≤ b < 10 har like mange gjeldende siffer som det er gjeldende siffer i b.
Eksempel: 2,83 · 10² har tre gjeldende siffer.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
Gjennomsnittsfart
Gjennomsnittsfarten er definert som:
Eksempel: En buss kjører 500 meter på 40 sekunder, hva er gjennomsnittsfarten?
, gjennomsnittsfarten er 12,5 meter i sekundet.
Gjentatt addisjon
Gjentatt addisjon er addisjon av samme tall flere ganger. Multiplikasjon kan sees på som gjentatt addisjon.
3 + 3 + 3 + 3 + 3 = 5 · 3 = 15
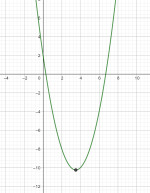
Globalt bunnpunkt
Et globalt bunnpunkt er det laveste punktet på grafen og det finnes kun ett.
En funksjon har et globalt bunnpunkt i , dersom for alle verdier av i hele definisjonsområdet.

Globalt toppunkt
Et globalt toppunkt er det aller høyeste punktet på en graf, og det finnes kun ett.
En funksjon har et globalt toppunkt i et punkt , dersom for alle verdier av i hele definisjonsområdet.
Grader
Grader er et mål for størrelsen til en vinkel. Vi bruker symbolet °.
En vinkel på 1° tilsvarer 1/360 av en hel sirkel. En rett vinkel er 90°.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Grenseinntekt
Hvor mye tjener vi dersom vi produserer en ekstra vare? Dette beløpet er grenseinntekten.
Grensekostnad
Hvor mye koster det å produsere én ekstra vare, når man har en bestemt produksjonsmengde.
Grenseverdi
En uendelig tallfølge a1, a2, a3, ...har grenseverdi A dersom vi kan få an så nær A vi vil ved å velge n stor nok.
Grunnlinje
Grunnlinja er en av sidene i en todimensjonal figur.
Alle sidene kan være grunnlinje. Når vi skal finne høyden i en trekant, må vi vurdere hvilken av sidene som er mest egnet som grunnlinje.
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Gruppe
En mengde G og en binær operator , som tilfredsstiller følgende aksiomer for alle x, y og z som tilhører G
1. xy er i G
2. (xy)z=x(yz)
3. ex=xe=x, e kalles en enhet
4. Det finnes en x* slik at xx*=x*x=e
Gruppen kalles Abelsk hvis den i tillegg er kommutativ, dvs.
5. xy=yx
Gunstig utfall
Et gunstig utfall er den hendelsen som er interessant for oss.
Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.
Se Hendelse
Gyldig
Begrepet gyldig brukes om blant annet modeller og løsninger i matematikk. Dersom en matematisk modell er gyldig, må den stemme overens med virkeligheten.
Eksempel: Vi skal løse en rasjonal likning
Vi multipliserer alle ledd med fellesnevneren:
abc-formelen gir løsningene . Men her er det viktig å være oppmerksom. For begge disse løsningene gir en nevner som blir 0. Derfor har denne likningen ingen gyldige løsninger.
Halvere
Halvere betyr å dele i to like store deler. Det er det samme som å dividere med 2.
Hastighetsvektor
Hastighet betenes med en vektor, gjerne , siden hastighet har en retning. Lengden på vektoren er farten.
Heltall
Heltall er de tallene vi oftest teller: 0, 1, 2, 3, 4... De hele tallene inkluderer også de negative tallene; -1, -2, -3...
Symbolet for mengden av hele tall er ℤ.
Hendelse
En hendelse eller begivenhet er en delmengde av utfallsrommet. En hendelse består av ett eller flere utfall.
Se Gunstig utfall
Histogram
Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.
Hjørne
Hjørnet i en todimensjonal figur er det punktet der to rette sidekanter møtes.
Hjørnet i en tredimensjonal figur er det punktet der tre eller flere sideflater møtes.
Hundredeler
Sifferet som står på hundredelsplassen viser hvor mange hundredeler det er i tallet.
Eksempel: 3,169. Her står sifferet 6 på hundredelsplassen.
Hundrer
Sifferet som står på hundrerplassen forteller hvor mange hundrere det er i tallet.
Eksempel: 38745. Dette tallet har 7 hundrere.
Hyperbel
Et kjeglesnitt som skjærer begge delen av en dobbeltkjegle. Et eksempel er grafen til funksjonen .
Hypergeometrisk fordeling
Hypergeometrisk fordeling er en sannsynlighetsfordeling man får når man gjennomfører et uordnet utvalg uten tilbakelegging av en mengde som inneholder to forskjellige elementer.
Matematisk skrives det med følgende formel:
Her er n antall elementer i mengden. m er antall elementer av en spesiell type, og er antallet av den andre typen. Vi trekker r elementer tilfeldig. X er antallet elementer av den typen vi er ute etter.
Eksempel: I en klasse er det 24 elever, 13 jenter og 11 gutter. Dersom vi trekker tilfeldig tre elever fra klassen, hva er sannsynligheten for at vi trekker nøyaktig 3 jenter?
Hypergeometrisk forsøk
Et hypergeometrisk forsøk har følgende egenskaper:
- Det er totalt n gjenstander av to (eller flere) typer.
- Antallet gjenstander av type 1 er og antallet gjenstander av type 2 er , slik at .
- Det skal trekkes et uordnet utvalg uten tilbakelegging av størrelse k.
Hyposykloide
Den kurven et punkt på en sirkel beskriver når sirkelen ruller på innsiden av en fast sirkel.
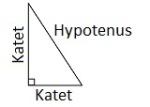
Hypotenus
Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter.
Hypotesetesting
Dette er en statistisk metode for å undersøke om en hypotese stemmer, og med hvilken sikkerhet vi kan si at denne hypotesen stemmer. For å finne ut dette stiller man opp to ulike hypoteser: en nullhypotese og en alternativ hypotese. Så gjennomfører man en undersøkelse og samler inn data. Man beregner sannsynligheten for å få et resultat gitt at nullhypotesen stemmer, dette kalles p-verdi. Dersom man beregner en svært lav p-verdi, er det veldig usannsynlig at nullhypotesen stemmer. Deretter må man velge et signifikansnivå, dette er sannsynligheten for at vi forkaster nullhypotesen selv om den er rett. Til slutt ser man om p-verdien er større eller mindre enn signifikansnivået. Dersom den er større enn signifikansnivået beholder man nullhypotesen, og dersom den er mindre forkaster man nullhypotesen.
Eksempel: Vi ønsker å finne ut om norske 16-åringer er høyere enn tidligere. Før har gjennomsnittshøyden til norske 16-åringer vært 170cm.
Da setter vi opp en nullhypotese
og en alternativ hypotese
Deretter må vi se på datamateriale av høyden til norske 16-åringer. Dersom datamateriale vårt gir en , må vi regne ut sannsynligheten for at vi får denne gjennomsnittshøyden tilfeldig, selv om nullhypotesen stemmer. Denne sannsynligheten kalles P-verdi. Hvis denne sannsynligheten er mindre enn et gitt signifikansnivå, f. eks 2%, kan vi forkaste nullhypotesen og påstå at . Dersom sannsynligheten er større enn signifikansnivået er vi nødt til å beholde nullhypotesen.
Høyde
Lengden av et linjestykke som står normalt på ei linje eller en flate.
Identitet
En matematisk identitet er en ligning som stemmer for alle variabler som inngår i ligningen. Ligningen er altså alltid oppfylt.
Eksempler: og
Ikke-numeriske data
Data som ikke er tall, for eksempel bokstaver, farger og gjenstander.
Ikke-standardiserte måleenheter
Måleenheter som ikke har en bestemt fastsatt størrelse, kalles ikke-standardiserte måleenheter.
Eksempler: armlengde, kopp, ansiktsbredde
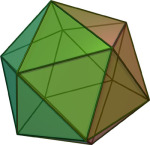
Ikosaeder
Et ikosaeder er ett av de fem platonske legemer og er satt sammen av 20 kongruente og regulære trekanter.
Implikasjon
En påstand impliserer en annen påstand hvis det følger at er sann hvis er sann. Vi skriver .
Eksempel: "Alle i klassen har gul t-skjorte" impliserer "Ingen i klassen har grønn t-skjorte".
Infinitesimal
En "uendelig" liten størrelse. Et viktig begrep i matematisk analyse. Brukes for eksempel til definisjon av og regning med differensialer og integraler.
Integral
Det bestemte integralet kan tenkes på som en uendelig sum av uendelig små størrelser. Integraltegnet er en utstrakt S for "sum", tallene a og b kalles grensene til integralet, f(x) kalles integranden og dx kalles differensialet til x.

Integralregning
Integralregning er forbundet med arealbegrepet. Et areal kan uttrykkes ved et bestemt integral, og det kan beregnes ved integrasjon. Integralet fra a til b av funksjonen f kan tolkes som arealet av det området som begrenses av funksjonens graf, x-aksen og de vertikale linjene x=a og x=b.
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
Intervall
Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).
Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.
Invers operasjon
En invers operasjon er en "motsatt" operasjon. Subtraksjon og addisjon representerer motsatte tankeprosesser, og de kalles inverse operasjoner. Divisjon og multiplikasjon er motsatte eller inverse regneoperasjoner.
Irrasjonale tall
Et reellt tall som ikke kan skrives som en brøk satt sammen av to heltall.
Eksempel: ,
Kardinaltall
Er et tall som angir et antall. Også kalt mengdetall.
Kartesisk koordinatsystem
Et koordinatsystem der aksene står vinkelrett på hverandre.

Katet
Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter.
Kjedebrøk
En brøk der nevner er et heltall og en brøk, hvis nevner igjen er et heltall og en brøk og så videre.
Eksempel:

Kjegle
En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.
Kjeksen til en kroneis har form som en kjegle.
Volum : V =
Overflate : A =
Kjeglesnitt
Et plant snitt av en kjegle og dette snittet blir en kurve som er løsningsmengden til en andregradslikning i to variable.
Der er fire typer glatte kjeglesnitt: sirkel, ellipse, parabel og hyperbel.
Koeffisient
Koeffisient er et tall, en konstant eller en funksjon som står som faktor i et matematisk uttrykk.
Eksempel: i uttrykket er koeffisienten til
Kombinatorikk
Handler om å finne antall mulige kombinasjoner i ulike sammenhenger.
Eksempel: antall måter å kombinere Lotto-tallene på, eller hvor mange ulike antrekk vi kan ha på oss dersom vi har 2 bukser og 3 skjorter.
Kombinatoriske problemer
Matematiske problemer som dreier seg om å finne antall mulige utfall eller antall kombinasjoner.
Eksempel: Karen Elise skal kjøpe kuleis med fire ulike smaker. I butikken er det totalt 12 forskjellige smaker på is, hvor mange kombinasjoner kan hun velge?
Her har vi et uordnet utvalg uten tilbakelegging:
, hun kan velge mellom 495 kombinasjoner.
Kommutativ ring
En ring der multiplikasjonsoperasjonen er kommutativ
Kommutative lov
Den kommutative lov for addisjon:
a + b = b + a
Den kommutative lov for multiplikasjon:
a · b = b · a
Kompleks funksjonsteori
Teorien for funksjoner definert for komplekse tall med komplekse tall som funksjonsverdier. Tilsvarende er reelle funksjoner definert for reelle tall og har reelle funksjonsverdier.
Kompleks variabel
En variabel som antar komplekse tall som verdier.
Komplekse funksjoner
Funksjoner definert for komplekse tall med komplekse funskjonsverdier.
Komplekse tall
Komplekse tall er en utvidelse av de reelle tall. De er satt sammen av en realdel og en imaginærdel. Tallene kan fremstilles i et tallplan hvor førsteaksen er de reelle tallene og andreaksen de imaginære tallene. Den imaginære enheten er . Et komplekst tall angis ofte på formen a + ib, hvor a og b er reelle tall.
Komplement
Komplementet til A, betegnet med , består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, .
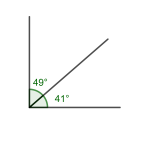
Komplementvinkler
To vinkler som til sammen er 90°.
Kongruens
Brukes både i algebra og i geometri.
I geometri: om figurer, for eksempel trekanter, som har parvis like vinkler og sider.
I algebra: om tall, for eksempel i regning modulo, et tall k om to tall som har samme rest etter divisjon med k.

Kongruensavbildning
En kongruensavbildning er en avbildning av en figur som bevarer alle avstander og derved alle vinkler. Avbildningen er en ny figur som er kongruent med figuren i utgangspunktet.
Se Kongruente figurer

Kongruente figurer
To figurer er kongruente dersom alle sider og alle vinkler er parvis like store. To kongruente figurer vil kunne dekke hverandre fullstendig om de plasseres oppå hverandre, det vil si at to figurer er kongruente når de har lik form og størrelse.

Konjugatsetningen
Konjugatsetningen kalles også tredje kvadratsetning:
.
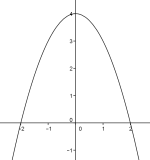
Konkav
La være en kontinuerlig funksjon. I de intervallene der grafen til åpner seg nedover, sier vi at er konkav. En kontinuerlig, deriverbar funksjon er konkav på et interval hvis har negativt fortegn for alle i intervallet.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Konstant prosentvis endring
Betyr at noe vokser eller minker med en viss prosentandel i løpet av en bestemt tidsperiode.
Eksempel: Renta i en sparekonto er på 1,05 %, dette innebærer at beløpet har økt med 1,05% etter et år. Altså er det en konstant prosentvis endring per år.
Kontinuerlig funksjon
En kontinuerlig funksjon er en sammenhengende graf, det vil si at grafen danner en sammenhengende kurve.
Kontinuitet
Brukes om en funksjon dersom grafen er sammenhengende. Gis i matematisk analyse en mer presis definisjon.
Kontinuum
Den ordnede mengden av de reelle tallene.
Kontinuumshypotesen
Hypotesen om at det ikke finnes noe kardinaltall mellom kardinaltallene for de rasjonale tallene og de reelle tallene.
Et kardinaltall er et tall som besvarer spørsmålet "hvor mange?", som for eksempel en, to, tre osv. Kardinaltall brukes også om antall elementer i en uendelig mengde, som mengden av de rasjonale tallene eller de reelle tallene. Kardinaltallet for mengden av reelle tall er størst av disse to, men fins det noe kardinaltall mellom dem?
Kontrapositiv
Av en gitt implikasjon "hvis P, så Q" kan man danne den kontrapositive implikasjonen "hvis ikke Q, så ikke P" ved å bytte om og negere premisset P og konklusjonen Q i den gitte implikasjonen. En implikasjon og dens kontrapositive er logisk ekvivalente.
Eksempel: "Et dyr som mjauer er en katt" er ekvivalent med det kontrapositive "Et dyr som ikke er en katt mjauer ikke".
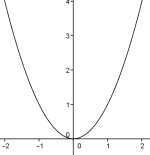
Konveks
La være en kontinuerlig funksjon. I de intervallene der grafen til åpner seg oppover , sier vi at er konveks. En kontinuerlig, deriverbar funksjon er konveks på et interval [a,b] hvis har positivt fortegn for alle i intervallet.

Konvekst polyeder
Et polyeder er konvekst hvis du kan legge det på en bordplate med hvilken som helst av sidene ned, og hele sideflaten er i kontakt med bordplaten.
Se Polyeder
Konvergens
Konvergens betyr i matematikk å nærme seg en grense.
Se Konvergent tallfølge
Konvergent tallfølge
En tallfølge konvergerer mot et tall k, hvis tallfølgen nærmer seg k som sin grense.
Eksempel:
Denne tallfølgen konvergerer mot 0, fordi tallene i følgen kommer nærmere og nærmere 0.
Koordinat
Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.
Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.
Se Koordinatsystem
Koordinatsystem
Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Korde
Et rett linjestykke som forbinder to punkter på en sirkel. Den lengste korden til en sirkel er diameteren.
Kostnadsberegning
Dette betyr at man regner ut totalprisen på noe. Det kan være et prosjekt, produksjon av varer/tjenester eller annet.
Eksempel: beregning av pris på et byggeprosjekt
Kredittkort
Et kredittkort er et betalingskort der den som bruker kortet får kreditt når kortet brukes. Dette vil si at selskapet som gir ut kortet låner ut penger til den som bruker det. Deretter betaler man tilbake det man har brukt innen en viss dato, kalt første forfall. Dersom man betaler senere, løper det renter på beløpet, og disse rentene er høye. Typiske rentesatser er mellom 23 og 30%. Kortene har også en grense for hvor mye penger man kan låne, dette kalles kredittgrense. Grensen er ofte mellom 50 000 og 200 000.
Eksempel: Man bruker 35 000 fra et kredittkort som har effektiv rente på 24,6%. Dersom man betaler ned i løpet av 12 måneder må man betale 39349. Altså har kredittkortet kostet 4349 i løpet av kun ett år. Det er altså dyrt å bruke kredittkort som et lån.
Kredittlån
Et kredittlån er en fellesbetegnelse for forbrukslån og kredittkort. Et lån uten sikkerhet kalles forbrukslån, og dette har høye renter i likhet med kredittkortet.Typiske renter er 15-20%, og dette er mye høyere enn andre lån der det stilles krav til sikkerhet. Lånebeløpene kan typisk være opp til 500 000,-.
Kritisk punkt
De kritiske punktene til en funksjon for er
1. Punkter der .
2. Punkter der ikke er definert.
3. Endepunktene til intervallet, og .
Kroneverdi
Kroneverdien forteller oss hvor mye én norsk krone er verdt ved ulike tider. Matematisk er kroneverdien omvendt proporsjonal med konsumprisindeksen:
Eksempel: Hvis man brukte én krone i 1939, hvilket beløp tilsvarer det i dag?
Fra Statistisk Sentralbyrå ser vi at konsumprisindeksen var 3,2 i 1939:
altså tilsvarte én krone i 1939 omtrent 31 kroner i dag.
Krumningsegenskaper
Krumningen til en funksjon er den dobbeltderiverte og forteller oss hvilken vei grafen til funksjonen "bøyer seg". Hvis den dobbeltderiverte er positiv, krummer grafen til funksjonen seg oppover, og hvis den dobbeltderiverte er negativ, krummer grafen seg nedover.
Kryptografi
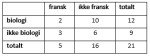
Krysstabell
En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
Kube
En kube er ett av de fem platonske legemer og er satt sammen av seks kongruente kvadrater.
For en kube med sidelengde a, er:
Volum = a3
Overflate = 6a2
Kubikkrot
Kubikkroten av et tall , skrevet , er det tallet som opphøyet i gir .
Eksempel: Kubikkroten av er , fordi .
Kubikktall
Et helt tall som kan skrives på formen n3.
Eksempel: 64 et kubikktall fordi .
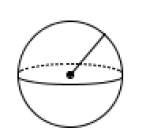
Kule
Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.
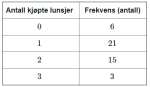
Kumulativ frekvens
Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Kumulativ relativ frekvens
Summen av alle de relative frekvensene som er mindre enn eller lik den aktuelle verdien. Også lik det tallet vi får ved å dele den aktuelle kumulative frekvensen på totalt antall data.
Se Relativ frekvens
Kurve
En kurve er en krum eller rett linje eller et linjestykke. En kurve har lengde, men ikke bredde eller dybde.
En kurve er en grafisk fremstilling av en ligning.
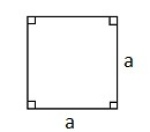
Kvadrat
En firkant der alle sider er like lange og alle vinkler 90°.
Kvadratrot
Kvadratrot har symbolet .
Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.
Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi . Det skrives .
Kvadrattall
Et kvadrattall er det positive heltallet som vi får når et heltall multipliserers med seg selv.
Eksempel: 25 er et kvadrattall, fordi
Kvadrere en sirkel
Betyr å finne et kvadrat som har samme areal som en gitt sirkel.
Kvartildifferanse
Differansen mellom første og tredje kvartil. Kalles også for kvartilbredden.
Kvartiler
Datasett deles inn i fire like deler og grensen mellom laveste og nest laveste firedel kalles første kvartil. Grensen mellom tredje og fjerde firedel kalles tredje kvartil. Andre kvartil er det samme som medianen.
Kvotient
Resultatet av en divisjon kalles en kvotient.
Eksempel: , her er 4 en kvotient.
Kvotient
I aritmetikk er en kvotient resultatet av en divisjon, for eksempel er kvotienten av 12 og 3 lik 4.Vi kan også ha en kvotient av for eksempel funksjoner, dvs. hvis f og g er funksjoner, kan vi danne kvotientfunksjonen f/g, der . For eksempel er kvotienten av uttrykkene 2 og 3x - 1 lik .
Ledd
I en addisjon kalles tallene som legges sammen for ledd.
Eksempel: , her kalles tallene 8, 3 og 5 for ledd.

Lemniskate
Lemniskaten er en lukket kurve som ser ut som et liggende 8-tall. Den kan i polarkoordinater angis
som r = p√(cos2θ).
Lemniskaten kan beskrives på liknende måte som ellipsen. Gitt to brennpunkter A og B med avstand 2a. Lemiskaten er da de punkter P som tilfredstiller at PA·PB = a2.
Lengde
Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.
Lengdeenhet
Måleenheten for lengde er meter med forkortelsen m. Andre lengdemål avledet av meter er: kilometer (km), desimeter (dm), centimeter (cm) og millimeter (mm).
Lie algebra
En ring eller algebra der den assosiative loven ikke gjelder. Lie algebraen har en operasjon kalt "Lie-bracket" som oppfyller regneregler som ligner på regnereglene for derivasjon.
Lie algebraer spille en viktig rolle for matematisk modeller i moderne fysikk.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.

Like vinkel
En vinkel på 180 grader kalles en like vinkel.
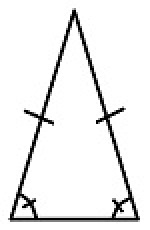
Likebeint trekant
I en likebeint trekant er to sider like lange og to vinkler like store.

Likesidet trekant
I en likesidet trekant er alle sidene like lange og alle vinklene 60°.
Likevekt og balanse
Se balanse og likevekt
Likeverdige brøker
Brøker som representerer samme verdi, men har ulike tellere og nevnere, kaller vi likeverdige brøker.
Eksempel: og er likeverdige brøker, fordi .
Likhetstegn
Likhetsteget har symbolet "".
Likhetstegnet forteller at det som står til venstre for likhetstegnet har samme verdi som det som står til høyre.
Eksempel:
Likningssett
Minst to likninger som inneholder de samme ukjente variablene. Likningssettene kan løses på flere forskjellige måter, blant annet innsettingsmetoden eller addisjonsmetoden.
Eksempel: Marco har kjøpt 9 frukt på butikken. Han har kjøpt epler til 6kr/stk og pærer til 5kr/stk. Prisen ble 49 kroner totalt. Hvor mange epler og hvor mange pærer har Marco kjøpt?
Vi stiller opp to likninger, der a står for antall pærer og b står for antall epler:
Deretter skriver vi om likning 1:
, og setter uttrykket inn i likning 2:
Marco kjøpte fire pærer og fem epler.
Lineære funksjoner
Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Lineære ligninger
Ligninger der alle de ukjente opptrer i første grad.
Eksempel:
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Linjediagram
Et linjediagram er en grafisk framstilling av data som er samlet over tid. Et punkt svarer til en observasjon på et bestemt tidspunkt. Det trekkes linjestykker mellom punktene.
Eksempel på bruksområde: aksjekurser, temperatur og salgsoversikter.
Linjestykke
Et linjestykke er en sammenhengende bit av en linje, avgrenset av to endepunkter. Navnet på et linjestykke er vanligvis gitt ved de to endepunktene: AB, CD, ...
Logaritme
Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.
Eksempel: log10(1000) = 3 ettersom 103 = 1000.
Logaritmefunksjon
Dette er funksjoner som inneholder logaritmer. Det kan være den naturlige logaritmen med grunntall e, eller logaritmer med andre grunntall, som regel grunntall 10.
Eksempler: , , er avbildet på figuren.
Logaritmelikning
En likning som inneholder en eller flere logaritmer.
Eksempler: ,
Logaritmetabell
Tabell med logaritmer med grunntall 10 av tall (med desimaler) mellom 1,0000 og 9 9999. Med logaritmer blir multiplikasjon omgjort til addisjon, så derfor ble disse tabellene brukt til beregning av
produkter av store tall. Bruken av logaritmetabeller forsvant med introduksjonen av lommekalkulatoren.
Logaritmisk spiral
En spiral er en kurve som snor seg om et fast punkt P. Beliggenheten til et punkt S på spiralen kan beskrives ved å angi retningen fra P til S angitt som vinkelen θ fra førsteaksen og avstanden fra P til S angitt som r. For en logaritmisk spiral tilfredstiller punktene på spiralen lnr = aθ, der a er et reelt tall.
Logisk algebra
Dette er den opprinnelige betegnelsen for boolsk algebra der variablene kun kan ha to verdier: 1 (sant) eller 0 (usant). De logiske operasjonene OG, ELLER og IKKE kan utføres på disse variablene. Boolsk algebra brukes blant annet til søk i databaser.
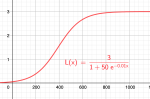
Logistisk vekst
Logistisk vekst kan beskrives helt generelt med en funksjon av typen:
Her er K, c og a positive konstanter. Når x øker, vil nevneren gå mot 1 og funksjonen nærmer seg konstanten K. Funksjonsverdien vil altså aldri bli større enn K, uansett hvor stor x blir.
Eksempel: Hvordan en populasjon vokser, kan beskrives med logistisk vekst. Figuren viser hvordan en funksjon som beskriver logistisk vekst kan se ut.
Lokalt bunnpunkt
Et lokalt bunnpunkt er det laveste punktet på grafen i et gitt område, og en graf kan ha flere lokale bunnpunkt.
En funksjon har et lokalt bunnpunkt i , dersom i alle nabopunktene til , altså alle punktene i et intervall rundt .
Lokalt toppunkt
Et lokalt toppunkt er det høyeste punktet på grafen i et gitt område, og en graf kan ha flere lokale toppunkt.
En funksjon har et lokalt toppunkt i , dersom for alle nabopunktene til , altså alle i et intervall rundt .
Løkker
En løkke brukes i programmering for å gjenta noe. Avhengig av løkken man bruker, kan man bestemme at løkken skal gjenta koden et bestemt antall ganger, eller helt til man har nådd et mål. Fordelen med løkker er at man slipper å skrive mange setninger med programkode.
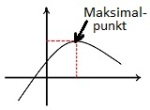
Maksimalpunkt
Et punkt der en funksjon har sin største verdi.
Se Toppunkt
Mangekant
En mangekant er en geometrisk lukket figur som er satt sammen av rette linjestykker. Kalles også en polygon.
Eksempel: trekant, firkant, femkant (pentagon) og sekskant (heksagon).
Masse
Massen til en gjenstand forteller oss hvor tung gjenstanden er. I dagligtale sier vi at en stein veier 3 kg. Det betyr at steinen har masse 3 kg.
Enheten til masse er kilogram (kg).
Matematikk
Matematikk og matematiker kan føres tilbake til det greske adjektivet mathematikos eller verbet manthanein. Det betyr "glad i å lære".
Matematikk ble tidligere oppfattet som læren om tall og geometriske figurer. I dag er det mer korrekt og generelt definert som vitenskapen om struktur, orden og sammenhenger.
Matematisk induksjon
En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:
- Bevis påstanden for n =1.
- Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).
Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Mengde
En samling av objekter en det samme som en mengde. Objektene som er i mengden blir gjerne kalt elementer. Matematisk skriver vi at et element er en del av en mengde på følgende måte: vil si at 's er et element i mengden B', , betyr 'q er ikke et element i mengden B'.
Eksempel: mengden av heltall på en terning kaller vi dermed er Klammeparentesen brukes når vi skriver opp elementene i mengden på listeform.
Mengdeteori
Teorien om mengder er et grunnleggende felt innen matematikk og logikk. En bestemt samling objekter kalles en mengde dersom en kan avgjøre om et gitt objekt tilhører mengden eller ikke. Mengdeteorien studerer hvordan mengder kan brukes til å bygge opp formelle strukturer i matematikk og logikk.
Meningsmåling
En meningsmåling er en spørreundersøkelse, hvor spørsmål kun stilles til et lite utvalg og ikke til alle aktuelle personer. På grunnlag av svarene til utvalget kan vi beregne ganske sikkert hvordan meningene er fordelt hos alle aktuelle personer.
Merverdiavgift
Merverdiavgift er en avgift vi betaler når vi kjøper varer eller tjenester og er inkludert i prisen til varen eller tjenesten.
25 % for de fleste varer eller tjenester
15 % for mat og drikke
12 % for persontransport, kinobilletter og utleie av rom
For oppdaterte satser se Skatteetatens hjemmeside.
Meter
Meter er måleenheten for lengde og forkortes m. Mange andre lengdemål er avledet av meter:
kilometer: 1 km = 1000 m
desimeter: 10 dm = 1 m
centimeter: 100 cm = 1 m
millimeter: 1000 mm = 1 m
Middelverdi
Se Gjennomsnitt
Middelverdisetningen
En setning om reelle funksjoner som sier at for enhver korde til grafen til en kontinuerlig og deriverbar funksjon fins det en tangent i et punkt mellom endepunktene som er parallell med korden.
Midtnormal
Midtnormalen til et rett linjestykke er den rette linja som går gjennom linjestykkets midtpunkt, og som står vinkelrett på linjestykket.
Midtspredning
Differansen mellom tredje og første kvartil kalles midtspredningen eller interkvartil variasjonsbredde. Kvartiler er et nyttig verktøy når man jobber med datamengder.
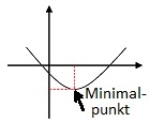
Minimalpunkt
Førstekoordinaten til et bunnpunkt kalles et minimalpunkt.
Minimumsdefinisjon
En minimumsdefinisjon betyr at man forklarer noe på enklest mulig måte. I matematikken har vi blant annet minimumsdefinisjoner av geometriske figurer.
Eksempel: Et kvadrat har fire like lange sider og alle vinklene er 90°.
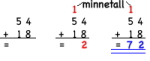
Minnetall
Ved summering av enerne (se bildet), får vi her 12. Tallet 12 kan ikke plasseres på enerplassen i svaret fordi tallet 13 består av en tier og to enere. Tieren må derfor settes over de andre tierne, og kalles minnetall. Dette minnetallet må summeres sammen med tierne.
Minste felles multiplum
Minste felles multiplum (MFM) er det minste tallet som flere hele tall går opp i.
Eksempel: Dersom vi skal finne minste felles multiplum av 8 og 18, starter vi med å faktorisere begge tallene: 8 = 2 · 2 · 2 og 18 = 2 · 3 · 3. I dette tilfellet blir MFM = 2 · 2 · 2 · 3 · 3 = 72, fordi 72 er det minste tallet både 8 og 18 går opp i, altså deres minste felles multiplum.
I minste felles multiplum finner du igjen faktorene til begge tallene.
Minste kvadraters metode
En tilnærmingsmetode som forsøker å tilpasse en funksjon til en polynomfunksjon, slik at gjennomsnittet av kvadratet av avstanden mellom de to funksjonene er minst mulig.
Minus
Se Subtraksjon
Modell
Se matematisk modell
Modellere
Å modellere vil si at man lager en matematisk modell. Man bruker matematikk for å beskrive virkeligheten.
Eksempler: økonomiske modeller, modeller for befolkningsvekst, fysiske modeller om klimaendringer
Modellering
Se modellere
Momentan vekstfart
Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet.
Monotoniegenskaper
En funksjon er monoton på et intervall hvis den er enten stigende eller avtagende på intervallet. Der en funksjon er stigende eller avtagende, er monotoniegenskapene til en funksjon.
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.
Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).
Multiplikasjonsregelen
Sannsynligheten for at flere bestemte uavhengige hendelser inntreffer etter hverandre er lik produktet av sannsynlighetene for hver enkel hendelse.
Eksempel: sannsynligheten for å få to seksere ved å kaste en terning to ganger er:
Multiplikasjonstegn
Regnetegnet for multiplikasjon er · .
Noen ganger kan du se multiplikasjonstegnet skrevet som x.
Eksempel: 2 · 3 eller 2 x 3
Myntenhet
Hvert land har sin egen myntenhet, sin egen valuta. Valutakursen (vekslingskursen) forteller hvordan vi kan veksle fra én myntenhet til en annen. I Norge er myntenheten kroner (NOK), i USA har de dollar, $, og i Storbritannia har de pund, £.
Mønster
Et mønster består av gjentakende elementer som er arrangert på en systematisk måte.
Ved å gjenkjenne mønsteret i for eksempel et tallmønster eller et figurmønster kan man finne de neste leddene i rekken.
Målestokk
Målestokk beskriver forholdet mellom en måleenhet i en modell og virkeligheten.
Eksempel: et kart kan ha målestokk 1:50 000 (leses: én til femtitusen).
- 1 cm på kartet tilsvarer 50 000 cm = 500 m i virkeligheten.
- 3 cm på kartet tilsvarer 3 · 50 000 = 150 000 cm = 1500 m i virkeligheten.
Måleusikkerhet
Måleusikkerhet er et tall som beskriver usikkerheten i et målt resultat. Måleusikkerheten beskriver hva det kan forventes at den sanne verdien er.
Følgende notasjon er vanlig: <målt verdi> ± <usikkerhet>
Eksempel: En lengde som måler 15 cm kan ha en måleusikkerhet på 0,5 cm. Da kan den sanne verdien forventes å ligge et sted mellom 14,5 cm og 15,5 cm. Notasjonen blir 15 cm ± 0,5 cm.
Målingsdivisjon
I målingdivisjon skal en gitt mengde deles inn i grupper som består av et visst antall.
Eksempel: En klasse med 28 elever skal deles i grupper med 4 elever i hver. Hvor mange grupper blir det?
4 går 7 ganger i 28, det betyr at vi får 7 grupper.
Måltall
Det tallet vi leser av på en linjal, en akse, en vekt eller liknende, kaller vi et måltall.
n-te roten
For et positivt tall og et tall , er n-te roten av , tallet slik at . Vi skriver . Hvis er et partall, må være et postivt tall.

Nabovinkler
To vinkler som ligger ved siden av hverandre, har et felles vinkelbein og utgjør 180° tilsammen.
Naturlige tall
De positive heltallene 1, 2, 3, 4...
Mengden av naturlige tall angis med symbolet .
Hvis 0 skal være med i mengden bruker vi symbolet .
Negative tall
Tall som er mindre enn null, kalles negative tall. Vi viser at tallet er negativt ved å sette — foran tallet.
Eksempel: , som leses minus tre.
Netto månedslønn
Lønnen du får utbetalt. Da er skatt, fagforeningskontigent og lignende trukket fra bruttolønna.
Nettoinntekt
Nettoinntekt er det samme som inntekt etter at fradragsberettigede utgifter som skatt og fagforeningskontigent er trukket fra.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Newton-Raphsons metode
Rekursiv metode der en gjennom suksessive approksimasjoner løser en likning på formen .
Først bestemmes et startpunkt . Tangenten til grafen i punktet skjærer x-aksen punktet som vi finner ved å bruke formelen . Prosessen gjentas ved å bruke som startpunkt. Generelt bestemmes fra etter formelen .
konvergerer mot en rot i likningen . Når prosessen avbrytes, får vi en tilnærmingsverdi.
Nominell lønn
Nominell lønn er det vi vanligvis bare kaller lønn.
Om du slår opp i en ordbok finner du følgende om ordene nominell;
- nominell
det er to måter å bruke ordet på
1 - som gjelder (bare) i navnet det er han som er lederen, iallfall nominelt
2 - pålydende obligasjonene har en nominell verdi på 1000 kr / nominell inntekt inntekt uttrykt i pengeverdien til enhver tid / nominell rente, til forskjell fra effektiv rente

Normal
En linje som står 90 grader på en annen linje.
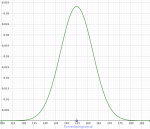
Normalfordeling
Normalfordelingen, som også kalles for Gauss-kurven, er en sannsynlighetsfunksjon som beskriver hvordan fordelingen av verdier for en stokastisk variabel X varierer, gitt forventningsverdien E(X) = µ og variansen Var(X) = σ2, der σ er standardavviket. Normalfordelingsfunksjonen er symmetrisk om µ.
Vi skriver normalfordelingen til X som: X ∼ N(μ,σ2)
Normalfordelingen har følgende funksjonsuttrykk
Eksempel: I en klasse er høyden til alle elevene målt. Normalfordelingen har forventningsverdi µ = 155 cm og standardavvik σ = 7,5 cm, og funksjonen er vist i figuren til høyre. Sannsynligheten for at en tilfeldig valgt elev er mellom 150 cm og 160 cm høy finner vi ved å beregne arealet under grafen mellom x = 150 og x = 160.
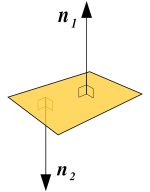
Normalvektor
En normalvektor for et plan står vinkelrett på alle linjer i planet.
Null
Null er tegnet for tom plass i posisjonssystemet. Null er noe som må finnes for å angi at ingenting finnes. Slik kan nullens magi beskrives.
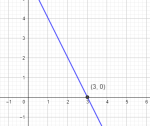
Nullpunkt
Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.
Numerisk analyse
Studie av metoder til å finne (tilnærmede) løsninger til forskjellige typer matematiske problem - ofte problem som ikke kan løses eksakt. Datamaskiner har stimulert dette fagområdet sterkt.
Numeriske data
En datamengde som består av tall.
Oddetall
Tallene 1, 3, 5, 7, 9 og 11 er eksempler på oddetall.
Oddetall er heltall hvor svaret ikke blir et heltall når de deles med 2.
Alle oddetall kan skrives på formen 2n+1, der n er et helt tall.
Et heltall som ikke er oddetall er partall.
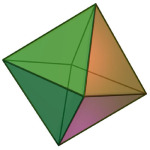
Oktaeder
Et oktaeder er ett av de fem platonske legemer og er satt sammen av åtte likesidede kongruente trekanter.
Omdreiningslegeme
Et omdreiningslegeme (rotasjonslegeme) fremkommer ved at en plan figur dreier seg om en akse i figurens plan. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate. Eksempler på omdreiningslegemer er kule, ellipsoide, sylinder og kjegle.

Omkrets
Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Omvendt funksjon, også kaldt invers funksjon
En funksjon ƒ har en omvendt funksjon ƒ-1 hvis den kan "reverseres". Vi har sammenhengen ƒ(x) = y hvis og bare hvis ƒ-1(y) = x. Vi har ƒ(ƒ-1(x)) = x og ƒ-1(ƒ(x)) = x. For eksempel hvis f(x) = 5x - 1 så er (Muntlig forklaring: "Hvis vi skal reversere funksjonen som tar et tall, ganger med 5 og så trekker fra 1, så må vi legge til 1 og dele på 5."
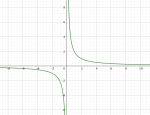
Omvendt proporsjonalitet
En omvendt proporsjonalitet er en funksjon på formen , der a er en konstant og x en variabel.
Når x øker vil verdien til funksjonen y avta.
Når x går mot 0 vil y-verdien gå mot uendelig.
Optimaliseringsproblemer
Å finne den beste løsningen blant alle mulige/gjennomførbare løsninger.
Ordinaltall
Det samme som ordenstall. Angir plass i en rekkefølge.
Eksempel: første, andre, tredje...
Ordnede utvalg
Når vi trekker objekter fra en samling og rekkefølgen vi trekker i er viktig, kalles dette for et ordnet utvalg.
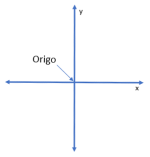
Origo
I et koordinatsystem står to akser vinkelrett på hverandre. Punktet der aksene møtes kalles origo. Origo har koordinatene (0,0).
Overflate
Med overflate av en tredimensjonal figur, for eksempel et prisme eller en sylinder, menes summen av arealene til alle flatene som den tredimensjonale figuren er satt sammen av.
Overslag
Brukes for å vite omtrent hvor mye noe vil koste eller hvor stort noe er. Overslag utføres ofte i hodet og tallene som inngår i regnestykket rundes av. Det finnes regler for avrunding, slik at forskjellen mellom nøyaktig svar og overslaget ikke blir for stort.
Fordi svaret ikke er nøyaktig, erstattes likhetstegnet med tegnet for tilnærmet lik .
Eksempel:
P-verdi
P-verdi er en sannsynlighetsverdi mellom 0 og 1. Verdien beskriver usikkerheten i trekningen av et utvalg. P-verdien brukes i hypotesetesting og er sannsynligheten for å få et likt eller et mer ekstremt testresultat enn det vi har fått hvis vi antar at nullhypotesen gjelder.
Eksempel: Hvis vi skal undersøke effekten av en medisin kan vi ikke teste hele befolkningen. Vi må gjøre et utvalg. Vi lager en nullhypotese som sier at medisinen ikke har noen effekt og antar at denne hypotesen stemmer. P-verdien sier noe om sannsynligheten for at dette utvalget mennesker gir resultater som viser at medisinen virker, gitt at nullhypotesen stemmer.
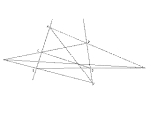
Pappus-problemet
Pappus' problemet ble vist av Pappus og kalles derfor Pappus' setning. Denne setningen har spilt en viktig rolle i utviklingen av geometri, og da særlig analytisk og projektiv geometri.
Pappus' setning sier at dersom hjørnene til en sekskant ABCDEF ligger vekselvis på to linjer, vil skjæringspunktene mellom diagonalene også ligge på linje.
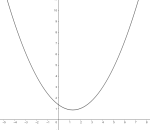
Parabel
Et kjeglesnitt med bare en symmetriakse. Et eksempel er grafen til funksjonen

Parallell
To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.
Tegnet som forteller at to linjer er parallelle:
Eksempel: , leses "linja g er parallell med linja f".
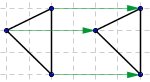
Parallellforskyving
Betyr å flytte alle punktene til en figur like langt og i samme retning. På denne måten flyttes (kopieres) hele figuren fra et sted til et annet.
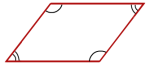
Parallellogram
Et parallellogram er en firkant med parvis parallelle sider. Vinklene er parvis like store.
Parameterframstillinger
Vi bruker parametre til å framstille/representere matematiske, og spesielt geometriske, størrelser. For eksempel er likningene x = , y = , der parameteren t ligger i intervallet en parameterframstilling av en sirkel.
Parametrisering
Å lage en parameterframstilling.
Parentesuttrykk
I et parentesuttrykk brukes parenteser for å multiplisere leddene i regneuttrykket.
Hvis et tall, en konstant eller en parentes står inntil en parentes, uten et matematisk symbol mellom, betyr det at vi skal multiplisere dem. Alle leddene i parentesen skal multipliseres.
Eksempel:
- 3(a+2) = 3⋅a + 3⋅2 = 3a + 6
- a(2a-3b) = a⋅2a - a⋅3b = 2a2 - 3ab
- (a+3)(2a-4b) = a⋅2a - a⋅4b + 3⋅2a - 3⋅4b = 2a2 - 4ab + 6a - 12b
Partall
Tallene 2, 4, 6, 8 og 10 er eksempler på partall.
Partall er heltall som delt med 2 gir et heltall som svar.
Alle partall kan skrives på formen 2n, der n er et helt tall.
Et heltall som ikke er partall er et oddetall.
Partielle differensiallikninger
Likninger som involverer funksjoner og deres partiell deriverte.
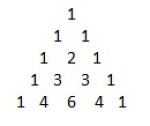
Pascals trekant
Tall satt sammen i en trekant med 1-ere i topp og langs sidekantene. De andre tallene i trekanten er lik summen av de to tallene som står ovenfor.
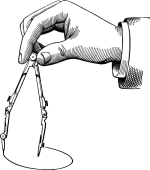
Passer
Passer er et tegneredskap som brukes til å tegne sirkler, slå buer eller måle nøyaktige lengder på linjestykker.
Perfekt kvadrat
Et perfekt kvadrat er et uttrykk som kan skrives som , altså at det er et eller annet i andre potens.
Perfekte tall
Et tall kalles perfekt hvis det er lik summen av tallets faktorer, der tallet selv ikke er medregnet.
Tallet 4 har faktorene 1, 2 og 4. Ser vi bort fra 4, blir summen 1 + 2 = 3. Tallet 4 er ikke et perfekt tall.
Tallet 6 har faktorene 1, 2, 3 og 6. Ser vi bort fra 6, blir summen 1 + 2 + 3 = 6. Tallet 6 er et perfekt tall.
De fire første perfekte tallene er 6, 28, 496 og 8128.
Personlig økonomi
Personlig økonomi er et tema innenfor skolematematikken der man regner på personlig inntekt, forbruk, lån og sparing, og setter opp regnskap og budsjett.
Perspektiv
Dybdevirkning, den måten noe tar seg ut på fra et bestemt sted. I perspektivtegning må en velge hvor en skal stå og se på motivet. Ofte forestiller man seg at motivet sees ovenfra.
Pi (π)
er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.
Plan
Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.
Plangeometri
Studiet av geometriske figurer i planet. I den analytiske plangeometrien studeres plane figurer ved bruk av koordinatsystem og algebraiske metoder. Læren om kjeglesnitt er et viktig emne innenfor plangeometri.
Plassverdisystemet
Når vi skriver et tall, har sifrene i tallet forskjellig verdi. Det er plassen til sifferet som bestemmer om det er enere, tiere eller hundrere osv.
Platonske legemer
Er det samme som regulære polyedere. Det vil si tredimensjonale objekter som er satt sammen av mangekanter som er likesidet og kongruente.
Det finnes fem platonske legemer, og alle har navn etter antall sideflater:
- Tetraeder
- Heksaeder (kube)
- Oktaeder
- Dodekaeder
- Ikosaeder
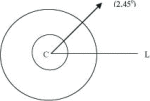
Polarkoordinater
Polarkoordinater består av en koordinat som er avstanden fra et valgt punkt og den andre koordinaten som er vinkelen til den valgte regningen.
La være de kartesiske koordinatene til et punkt og polarkoordinatene til samme punktet. Da er
og den andre veien
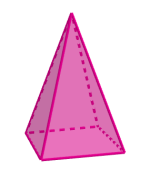
Polyeder
En tredimensjonal figur sammensatt av et endelig antall plane flater som kalles sideflater.
Eksempel: en pyramide er et polyeder med fire eller fem sideflater. Et rett prisme er også et polyeder.
Regulære polyedre kalles platonske legemer.
Se Platonske legemer.

Polygon
Er det samme som en mangekant.
Se Mangekant.
Polygonale tall
En generalisering trekanttall og kvadrattall. Polygontallene teller antall punkter organisert i et bestemt mønster i et polygon.
Trekanttallene er 1,3,6,10,15,...
Kvadrattallene er
1,4,9,16,25,...
Pentagonaltallene er
1,5,12,22,...
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Polynomdivisjon
Med polynomdivisjon mener vi å dividere på polynomer i stedet for på tall. Polynomdivisjon kan brukes til å faktorisere polynomer.
Eksempel:
- Vi kan også skrive (2x2-4x-6) : (x-3) = 2x + 2.
- Vi kan bruke resultatet over til å faktorisere polynomet med høyest orden og får at 2x2-4x-6 = (2x+2)(x-3).
Polynomfunksjon
En funksjon som har et polynom som funksjonsuttrykk kalles for en polynomfunksjon.
Eksempel: 2x3 - 3x2 - 5x + 2.
Ettersom 2x3 er det leddet med den høyeste eksponenten (3), har vi en tredjegradsfunksjon. Vi ser grafen til polynomfunksjonen til høyre.
Polynomlikning
En likning der bare summer og produkter av en eller flere ukjente og konstanter forekommer.
Populasjon
En samling av individer eller objekter som har noen felles egenskaper.
Eksempel: menneske, hare, smørblomst
Positive tall
Tall som er større enn null kalles positive tall.
Eksempel: 1, 78, 435.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Potensiell teori
Teorien om potensialfunksjoner, som er en generalisering av integralfunksjoner i flere variable.
Primtall
Positive hele tall større enn 1, som kun er delelig med 1 og seg selv.
Ti fem første primtallene er: 2, 3, 5, 7, 11.
Primtallsfaktorisering
Er å skrive et tall som et produkt av primtall.
Eksempel:
Prisindeks
Prisindeks brukes til å beskrive hvordan prisen på en vare eller tjeneste har utviklet seg. Prisindeksen angir forholdet mellom prisen på to forskjellige tidspunkt, for eksmpel prisen nå sammenlignet med prisen et basisår.
Følgende formel kan brukes til å finne prisindeks:
der ny pris er prisen ved tidspunktet du ønsker å finne prisinndeksen til, basisindeks er prisindeksen i basisåret og basispris er prisen i basisåret.
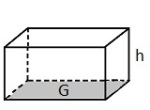
Prisme
Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.
Har et prisme grunnflate G og høyde h, er volumet lik G · h.
Problemløsing
Problemløsing er en matematisk metode som handler om å bruke den matematikken vi allerede kan til å utvikle egne strategier for å løse ukjente matematiske problemer.
Problemløsningsstrategi
Når man jobber med problemløsing utvikler man egne planer for hvordan man skal gå frem for å løse et ukjent problem. En slik plan, eller strategi, kalles for en problemløsningsstrategi.
Produkt
Produkt er et resultat av en multiplikasjon.
Eksempel: 2 · 7 = 14
14 er produktet, mens 2 og 7 kalles faktorer.
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
Prognose
En prognose er en begrunnet gjetning/forutsigelse om hva som kommer til å skje i framtiden. For å lage en prognose ser man på data og prøver å finne ut det mest sannsynlige utfallet i framtiden.
Programmere
Se Programmering
Programmering
Programmering er en prosess der man skal løse et problem gjennom å skrive en kode som skal forstås av en datamaskin. I prosessen må personen som programmerer identifisere det gitte problemet, tenke ut mulige løsningsstrategier, skrive koden inn på datamaskinen og eventuelt lete etter feil i koden slik at den stadig kan forbedres.
Projektiv geometri
En gren av geometrien som ble utviklet på 1700- og 1800-tallet. Delvis inspirert av perspektivtegning, og er en utvidelse av Euklids plan- og romgeometri som tar med uendelig fjerne punkter. Dermed er parallelle linjer i planet linjer som møtes i et uendelig fjernt punkt.
Promille
Promille betyr tusendel og skrives ‰.
Promille brukes til å måle konsentrasjoner og vektenheter. Dersom en person har 1,0 alkohol i blodet betyr det at dersom alt blodet i kroppen ble delt i tusen deler som alle veide like mye, så ville en av disse delene tilsvare ren alkohol.
For å regne om fra prosent til promille multipliserer man med 10.
For å regne om fra promille til prosent dividerer man med 10.
Regnereglene for promille er tilsvarende de for prosent, med den forskjell at man forholder seg til 1000 i stedet for 100.
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
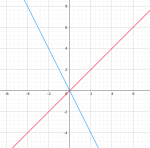
Proporsjonalitet
En proposjonalitet er en funksjon som har formen y = ax. Funksjonen går gjennom origo og er en lineær funksjon.
Hvis stigningstallet a er positivt vil en proporsjonal funksjon y øke når x øker. Se rød linje der a = 1.
Hvis stigningstallet a er negativt vil y avta når x øker. Se blå linje der a = -2.
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Prosentfaktor
En prosentfaktor er et prosenttall skrevet om til et desimaltall.
Eksempel: 32 % blir skrevet som 0,32 når det skal skrives som en prosentfaktor.
Prosentpoeng
Prosentpoeng er forskjellen mellom to prosenttall.
Eksempel: Forskjellen mellom og er 2 prosentpoeng.
Prosentpoeng
Prosentpoeng angir endringen mellom to prosenttall:
nytt prosenttall - opprinnelig prosenttall = prosentpoeng
Eksempel:
- En endring fra 40 % til 47 % har en økning på 7 prosentpoeng.
- En endring fra 35 % til 30 % har en nedgang på 5 prosentpoeng.
Punkt
I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

Pyramide
Et objekt som består av en mangekantet grunnflate, med sideflater som er trekantede. Trekantene møtes i en spiss som utgjør et hjørne av pyramiden.

Pytagoras læresetning
Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
Pytagoreiske tripler
Talltripler som forekommer som lengdene til sidekantene i en rettvinklet trekant.
Eksempel: 3, 4 og 5 er en trippel, fordi . Et annet eksempel er 5, 12 og 13.
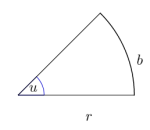
Radianer
Det absolutte vinkelmålet til vinkelen er tallet der er buelengden og er radien. Legg merke til at siden både og er lengder, vil lengdebenevningene forkortes mot hverandre i brøken , slik at det absolutte vinkelmålet blir et ubenevnt tall. Likevel sier vi ofte at er målt i radianer.
I en sirkel med radius er omkretsen lik . Det er derfor naturlig å si at en runde i sirkelen tilsvarer radier eller radianer.

Radius
Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.
Rasjonal eksponent
Vi kaller en eksponent på formen for en rasjonal eksponent. Potenser med rasjonal eksponent kan skrives som rottuttrykk:
, der a > 0 hvis n er et partall.
Eksempel:
- . Hvis n = 2 skriver vi ikke n over rottegnet.
- . Hvis n > 2 skriver vi n over rottegnet.
Rasjonal funksjon
En funksjon som er en kvotient av to polynomfunksjoner.
Rasjonale eksponenter
Et uttrykk med rasjonale eksponenter betyr at vi har et rasjonalt tall i en eksponent, for eksempel der m og n er hele tall og n forskjellig fra 0. Vi har der er løsningen til når n er et oddetall, og den positive løsningen til når n er et partall og .
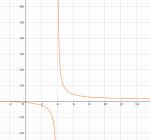
Rasjonale funksjoner
Hvis et funksjonsuttrykk er skrevet som en brøk som gir forholdet mellom to polynomer kalles den for en rasjonal funksjon.
Rasjonale funksjoner er på formen: der G(x) og H(x) er polynomfunksjoner. f(x) er ikke definert for H(x) = 0.
Eksempel: Grafen til funksjonen er vist i figuren til høyre. f(x) er ikke definert for x=4 og vi ser et brudd i grafen.
Rasjonale tall
Et tall som kan skrives som en brøk på formen der m og n er hele tall og n forskjellig fra 0. Mengden av rasjonale tall er ℚ.
Eksempel:
0,42, kan skrives som
2, kan skrives som
Reallønn
Reallønn er verdien av lønnen, etter at prisutviklingen har blitt tatt hensyn til. Reallønn sier altå noe om hvor stor den nominelle lønnen er i forhold til samfunnets prisnivå.
Realverdi
En virkelig eller reell verdi. En gjenstand sin verdi uttrykt ut fra et konstant prisnivå.
Reelle tall
Tall som kan markeres på en tallinje. Mengden av reelle tall er ℝ.
Eksempel: Alle heltall, alle rasjonale tall og alle irrasjonale tall.
Regneark
Regneark er et type digitalt verktøy man kan bruke til å struktrere data. Vi kan skrive inn formler for å gjøre utregninger i det digitale rutearket. I regneark kan man lage forskjellige typer diagrammer og grafer for å presentere både små og store mengder data.
Regnestrategi
En regnestrategi er en strategi eller en metode man kan bruke når man skal regne med matematiske symboler som .
Forskjellige måter å tenke på gir forskjellige regnestrategier, men samme svar.
Eksempel: Du hadde 58 kroner før du kjøpte en ball til 21 kroner. Hvor mange kroner har du igjen?
- 50 minus 20 er 30, og 8 minus 1 er 7. Ved å legge sammen 30 + 7 får vi 37.
- 21 pluss 9 er 30. 30 pluss 20 er 50. 50 pluss 8 er 58. Så 9 + 20 + 8 som blir 37.
- Med begge regnestrategiene ser vi at du har 37 kroner igjen.
Regneuttrykk
Et regneuttrykk har vi når vi setter sammen tall og/eller bokstaver med regnetegn. Tekstoppgaver kan for eksempel skrives om til regneuttrykk.
Eksempel: Det er 5 pizzastykker igjen. Du og vennen din spiser et hvert. Hvor mange pizzastykker har du igjen? Regneuttrykket blir da: 5-1-1 = 3.
Et sammensatt regneuttrykk er et regneuttrykk som består av flere forskjellige regnetegn. Her er det viktig å tenke på regnerekkefølgen.
Eksempel: Du hadde 150 kroner men ga bort 50. Faren din dobler pengene du har igjen. Hvor mye penger har du nå? Det sammensatte regneuttrykket blir da.
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.

Regulær mangekant
En mangekant der alle sidene er like lange og alle vinklene er like store.
Regulære polyedre
Polyedre der alle sideflatene er like og alle vinklene er like store. Kalles også Platonske legemer. Det finnes nøyaktig fem forskjellige: Tetraeder, heksaeder (kube), oktaeder, dodekaeder og ikosaeder.

Regulært polygon
En mangekant der alle sidene er like lange og alle vinklene er like store.
Rekke
Summen av alle tall i en tallfølge. Rekka kan være endelig eller uendelig.
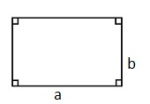
Rektangel
Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:
Omkrets:
Rekursiv formel
Dersom vi har en rekke med tall og kan bruke et tall i rekken til å bestemme det neste leddet har vi en rekursiv formel. Vi trenger altså informasjon om det forrige leddet.
La n være leddets plassering og an være verdien til ledd nummer n. Hvis verdien an-1 er kjent og vi kjenner til forholdet mellom an-1 og an har vi en rekursiv formel.
Eksempel: Vi har følgende tallrekken a1 = 1, a2 = 2, a3 = 3 og a4 = 4. Vi ser her at
- a2 = a1 + 1 = 2, a3 = a2 + 1 = 3 og så videre.
Den rekursive formelen for denne tallrekken blir da an = an-1 + 1
Rekursive sammenhenger
En rekursiv sammenheng binder sammen et begrep med seg selv. En tallfølge kan angis med en rekursiv formel som binder sammen et eller flere ledd i følgen med et annet ledd i følgen, for eksempel kan oddetallene angis med formelen . Formelen gir en rekursiv sammenheng mellom leddene i følgen, og sier hvodan vi kan regne ut det neste leddet ved hjelp av det foregående.
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Rente
Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger.
Se renteformel og rentefot
Renteformel
Renteformelen kan skrives slik:
der r står for rentebeløpet, K for kapitalen, p for rentefoten og d for det antall dager kapitalen forrentes.
Rentefot
Når du låner penger i en bank betaler du lånet tilbake med renter.
Det som bestemmer hvor mye du må betale i renter er rentefoten (rentesatsen), størrelsen på beløpet og tiden du låner.
Rentefoten er en viss prosent av lånebeløpet.
p brukes ofte som symbol for rentefot.
Dersom du har et innskudd i banken, tjener du penger i form av renter. Da er det du som låner penger til banken.

Representasjon
En matematisk representasjon er en fremstilling av matematiske objekter. Slike representasjoner kan for eksempel være skriftlige, fysiske eller visuelle.
Eksempel:
- Skriftlig ved bruk av symbol:
- Fysisk ved bruk av gjenstand: 12 kuler deles mellom 4 personer
- Visuelt ved bruk av figur: en tabell med 12 ruter fargelegges med 4 farger. Se til høyre.
Residuer
Brukes til å forenkle beregning av integraler av spesielt komplekse funksjoner. Residuen til en funksjon f(z) i et punkt a er grenseverdien til (z-a)f(z) når z går mot a.
Resonnere
Å resonnere betyr å tenke seg frem til en fornuftig løsning på et problem eller en strategi for å løse en oppgave. Dette innebærer å følge en logisk tankerekke og jobbe steg for steg mot en løsning på problemet.
Rest
En rest er noe som blir til overs. Når en divisjon ikke går opp, blir noe til overs og dette kalles for rest.
Eksempel: deler vi 7 bananer på 2 personer, får hver av dem 3 bananer og 1 banan blir til overs. Denne bananen er rest.

Retningsvektor
En linje går gjennom punktet og er parallell med vektoren . Vektoren kalles for retningsvektoren for linja.
Rett vinkel
En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Riemannflate
En lukket flate med kompleks struktur. Først studert systematisk av Riemann. Siden har disse flatene hatt en helt sentral plass i geometrien.
Ring
En mengde med to operasjoner, gjerne addisjon og multiplikasjon, som oppfyller de vanlige regnereglene, bortsett fra at multiplikasjonen ikke trenger være kommutativ.
Tallene 0 til 11 danner en ring dersom en regner modulo 12 (som på klokka). Her er multiplikasjonen kommutativ.
Romertall
Romertallene stammer fra Romerriket, og de brukte noen få bokstaver til å betegne tall.
Tallet 1 ble skrevet med bokstaven I, tallet 5 ble skrevet med bokstaven V og tallet 10 ble skrevet med bokstaven X.
Et tall ble skrevet ved å sette flere bokstaver etter hverandre. Man begynte med de høyeste verdiene slik at verdiene kunne adderes.
Eksempel: XXVII = 10 + 10 + 5 + 1 + 1 = 27
Setter man en mindre verdi foran en større, skal den minste verdien trekkes fra den større.
Eksempel: XXIV = 10 + 10 + (5 -1) = 24
Romertallene:
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
Rommål
Rommål er det samme som volum.
Se Volum
Rot
Se Kvadratrot
Rotasjon
En figur i planet, kan roteres rundt et punkt. Et objekt i rommet kan roteres rundt en akse.
Du kan for eksempel dreie et linjestykke 90 grader mot klokka, eller rotere en trekant 180 grader.
Rotuttrykk
Rotuttrykk er potenser med en brøk som eksponent, det vi kaller rasjonale eksponenter. Når vi tar roten av et tall a finner vi tallet b som gir a hvis vi ganger b med seg selv n ganger.
Rotuttrykk skrives på formen:
Eksempel: La a = 9 og n = 2. √9 = 3 ettersom vi får 9 hvis vi ganger 3 med seg selv n = 2 ganger.
Dersom n > 2 skriver vi n over rottegnet. Hvis n = 2 lar vi rottegnet stå uten å skrive 2 som en del av rottegnet.
Sammensatt funksjon
I en sammensatt funksjon er et funksjonsuttrykk satt inn i et annet. En sammensatt funksjon har formen: f(g(x))
Funksjonen f avhenger av funksjonen g.
Eksempel:
- f(x) = x2-1
- g(x) = 2x+1
- f(g(x)) = (2x+1)2-1
Sammensatte måleenheter
Når grunnleggende enheter for måling, grunnenheter, settes sammen til nye enheter får vi det som kalles sammensatte måleenheter.
Eksempel: m/s eller g/L
Sammensatte tall
Tall som er delelige på andre tall enn seg selv og 1, kaller vi sammensatte tall. Sammensatte tall kan skrives som produkt av primtall.
Eksempel:
6 = 2 · 3
27 = 3 · 3 · 3
55 = 5 · 11
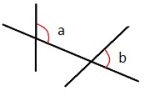
Samsvarende vinkler
To vinkler som enten har venstre vinkelben eller høyre vinkelben felles. Samsvarende vinkler behøver ikke være like store.
Eksempel: ∠a og ∠b er samsvarende vinkler, fordi de har høyre vinkelben felles.
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
Sannsynlighet med tilbakelegging
Fra et utvalg trekker vi en tilfeldig gjenstand. Hvis vi legger tilbake gjenstanden før vi trekker neste, sier vi at forsøket er gjort med tilbakelegging.
Eksempel: Du skal trekke to kuler fra ei eske. Det er 5 røde og 5 blå kuler i eska. Du trekker en kule og noterer resultatet. Før du trekker neste kule, må den første legges tilbake i eska. Du har fortsatt 5 røde og 5 blå kuler i eska.
Sannsynlighet uten tilbakelegging
Fra et utvalg trekker vi en tilfeldig gjenstand. Hvis vi ikke legger tilbake gjenstanden før vi trekker neste, sier vi at forsøket er gjort uten tilbakelegging.
Eksempel: Du skal trekke to kuler fra ei eske. Det er 5 røde og 5 blå kuler i eska. Du trekker en kule og noterer resultatet. Du legger ikke kula tilbake i eska. Det vil si at det er 9 kuler i eska før du trekker neste kule.
Sannsynlighetsfordeling
Sannsynlighetsfordeling er en teoretisk fordeling som beskriver hvordan en stokastisk variabel er fordelt og angir sannsynligheten for hvert mulige utfall.
Eksempel: Binomisk fordeling, hypergeometrisk fordeling og normalfordeling.
Sannsynlighetsmodell
Oversikten over alle mulige utfall og sannsynligheten for hvert av dem i et forsøk kalles for en sannsynlighetsmodell.
Eksempel: Sannsynlighetsmodellen for kast med én terning er vist i tabellen under.
Dette er en uniform sannsynlighetsmodell ettersom sannsynligheten for hvert utfall er like stor.
Sannsynlighetsteori
Undersøkelser av mulige utfall av gitte begivenheter sammen med deres relative sannsyligheter og forekomster. Det er faktisk betydelig uenighet omkring nøyaktig hva sannsynlighet betyr i praksis. Noen matematikere anser det bare som en komponent i en abstrakt teori, mens andre gir det en tolkning basert på frekvensen av visse utfall.

Sekant
En linje som skjærer en kurve. En korde er en del av en sekant. En sekant er ikke det samme som en tangent.
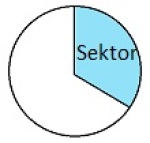
Sektor
En sektor er en del av en sirkel, et område som er avgrenset av to radier og en sirkelbue. En sektor har form som et kakestykke.
Sektordiagram
Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.
Semiregulære polyedre
Polyedre der alle sideflater er regulære mangekanter, og alle hjørner er like.
Se Platonske legemer
Sentralgrensesetningen
La n være antallet uavhengige stokastiske variabler X1, X2, ... Xn. Hvis alle X1, X2, ... Xn har samme forventningsverdi μ og standardavvik σ sier sentralgrensesetningen at summen av alle de stokastiske variablene X = X1 + X2 + ... + Xn er tilnærmet normalfordelt med forventningsverdi E(X) = n⋅μ og standardavvik .
Sentralmål
Sentralmål er utregnede verdier som viser "sentrum" for innsamlede data. Tre eksempler på sentralmål er gjennomsnitt, median og typetall.
Se gjennomsnitt, median og/eller typetall
Serielån
Serielån er et lån som betales tilbake med like store avdrag hver termin. I tillegg til avdrag må du betale renter. Serielånet har høyere terminbeløp i begynnelsen av tilbakebetalingsperioden og lavere mot slutten, fordi rentebeløpet blir lavere og lavere.
Sfære
En sfære er en kule og er definert som alle punktene i rommet med en fast avstand, r, fra et fast punkt.
Side
Siden (eller sidekanten) i en figur er en rett linje som forbinder to nabohjørner.
Siffer
Er symbolene (skrifttegnene) som vi bruker i vårt posisjonssystem for å beskrive ulike tall.
Vi har ti ulike siffer: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Simulere
Se simulering - statistikk
Simulering - statistikk
I matematikk handler simulering om å gjenskape eller etterligne en situasjon som tar for seg matematiske problemstillinger. Man kan simulere for å spare tid eller for å etterligne situasjoner man ikke får til med de midlene man har tilgjengelig.
Eksempel: Hvis man skal undersøke 5000 terningkast kan det være hensiktsmessig å simulere situasjonen ved hjelp av programmering i stedet for å kaste terningen 5000 ganger og skrive ned alle observasjonene.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
Sinussetningen
Er en setning som sier at forholdet mellom sinus til vinklene i en trekant og deres motstående sider er konstant.
La være en trekant, og la og være vinklene i trekanten. Da er
Vi vil også ha nytte av følgende formulering:

Sirkel
Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.
Areal:
Omkrets:
Sirkelbue
Er en sammenhengende del av sirkellinjen.
Sirkelsektor
Se Sektor
Skalarprodukt
Kalles også prikkprodukt. Hvis og er to vektorer i planet, definerer vi skalarproduktet mellom dem algebraisk som . Produktet er en skalar (et tall), derav navnet. Geometrisk har vi der v er vinkelen mellom vektorene,
. Prikkproduktet kan defineres tilsvarende i høyere dimensjoner.
Skatt
Skatt er en avgift som stat og kommune pålegger den enkelte borger å betale.
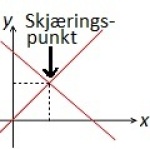
Skjæringspunkt
Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
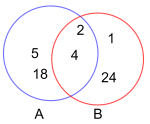
Snitt
Snittet av to mengder A og B er en ny mengde som består av alle elementer som forekommer både i A og B.
Eksempel:
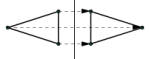
Speile om en linje
Å speile en figur om en linje, betyr å tegne den samme figuren på den andre siden av linjen, slik at alle punkter i figur 1 har samme avstand til linjen som tilsvarende punkter i figur 2.
Figurene vil dekke hverandre helt hvis vi bretter arket langs denne linjen.

Speile om et punkt
Å speile om et punkt betyr å tegne den samme figuren rotert 180° rundt punktet. Hvert punkt i figur 1 har samme avstand fra roteringspunktet som tilsvarende punkter i figur 2.
Spilldesign
Spilldesign handler om å lage spill, bestemme hvordan spillet skal se ut, lage reglene og bestemme hva som er målet med spillet. I spilldesign kan det være viktig å tenke gjennom hvert ledd grundig, og undersøke hvordan ulike valg påvirker resten. Algoritmsik tenking står sentralt i spilldesign.
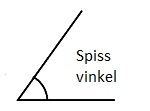
Spiss vinkel
En spiss vinkel er mellom 0° og 90°.

Spissvinklet trekant
Trekant der alle vinklene er spisse, dvs. alle vinklene er mellom 0° og 90°.
Spredningsmål
Spredningsmål er størrelser som sier oss noe om hvor mye dataene i et datasett varierer. Noen eksempler på spredningsmål er variasjonsbredde, varians og kvartiler.
Stambrøk
En stambrøk er en brøk der teller er lik en.
Eksempel:
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Standardiserte måleenheter
Måleenheter som har en bestemt, fastsatt størrelse kalles for standardiserte måleenheter. Slike måleenheter er felles for alle.
Eksempel: SI-systemet er et internasjonalt system med standardiserte måleenheter. Blant SI-enhetene har vi meter, kilogram og sekund.
Stasjonært punkt
Et stasjonært punkt for en funksjon er et punkt der den deriverte til funksjonen er null, .
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
Statistisk datamateriale
I statistiske undersøkelser samler man inn opplysninger, eller statistisk datamateriale, som man ønkser å undersøke nærmere. Statistisk datamateriale forbindes ofte med tallverdier, men kan også være bokstaver eller gjenstander. Vi kaller slik data for ikke-numerisk data.
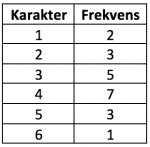
Statistisk fordeling
En statistisk fordeling er en observert fordeling som gir oversikt over hvordan verdiene i et statistisk datamateriale er fordelt. Fordelingen kan presenteres med absolutte tall eller som prosent, og man ser nøyaktig hvordan datamaterialet er fordelt.
Statistiske framstillinger
Statistiske framstillinger er representasjoener av statistisk datamateriale. Hvilken måte man velger å framstille datamaterialet på avhenger av hva slags data som skal presenteres. Forskjellige måter å framstille statistisk data på er for eksempel sektordiagram, søylediagram og linjediagram.
Statistiske undersøkelser
I statistiske undersøkelser samler man inn opplysninger, organiserer den innsamlede dataen på en oversiktlig og praktisk måte, tolker datamaterialet og trekker konklusjoner fra dette.

Stigningstall
Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Stokastisk forsøk
Dersom vi gjennomfører et forsøk og ikke vet hva utfallet blir, men vet hva de mulige utfallene ved forsøket er, har vi et stokastisk forsøk. I et stokastisk forsøk vet vi sannsynligheten for hvert utfall, eller så kan vi finne sannsynligheten for at hendelsene inntreffer.
Eksempel: Kast av terning er et stokastisk forsøk. Kaster vi en terning vet vi ikke på forhånd hvor mange øyne terningen viser. Det vi vet er at kastet vil resultere i 1, 2, 3, 4, 5 eller 6 øyne, ettersom dette er de mulige utfallene ved et terningkast. En terning har ikke færre eller flere øyne enn dette.
Stokastisk variabel
En stokastisk variabel er en variabel som har en tallverdi. Verdien til den stokastiske variabelen bestemmes av de mulige utfallene av et stokastisk forsøk.
Eksempel: Vi kaster to kronestykker og har følgende utfallsrom: U = {KK, MK, KM, MM}. K er kron og M er mynt. Vi velger Z = antall mynt. Ettersom Z beskriver en tallverdi i det mulige utfallsrommet U, er Z en stokastisk variabel.
- P(Z = 0). Sannsynligheten for å få null mynt.
- P(Z = 1). Sannsynligheten for å få nøyaktig én mynt.
- P(Z 1). Sannsynligheten for å få én eller flere mynt.
Stolpediagram
Et søylediagram uten bredde på søylene.
Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak.
Se Søylediagram
Strategi
En strategi er en plan for gjennomføring for å nå et bestemt mål. Samme oppgave kan løses med forskjellige strategier.

Stråle
En stråle er en rett linje som starter i et punkt, men som ikke har noen begrensning i den andre retningen.

Stump vinkel
En stump vinkel er mellom 90° og 180°.
Substitusjon, også kalt variabelskifte
En metode for å antiderivere/integrere et uttrykk. Vi utnytter blant annet kjerneregelen for derivasjon baklengs, så hvis vi gjenkjenner en kjerne, er det gjerne den vi velger som ny variabel. For eksempel hvor vi substituerer/skifter variabel: u = 4x.
Subtraksjon
En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen.
Sum
Resultatet av en addisjon.
Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.
Summere
Er et annet ord for å addere, eller å "legge sammen" tall.
Se Sum
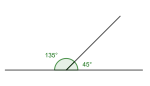
Supplementvinkler
To vinkler som til sammen er 180°.

Sykloide
En kurve som beskrives av et fast punkt på en sirkel, når denne ruller på en rett linje.
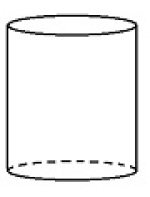
Sylinder
En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.
Symmetri
Symmetri er et mønster som gjentar seg. Vi kan ha symmetri om et punkt, en linje eller et plan.
Symmetri om en linje, betyr at hvis vi bretter langs linjen vil mønsteret på begge sidene dekke hverandre helt.
Dersom man speiler en figur om en linje, et punkt eller et plan oppnår man symmetri.
Symmetriske funksjoner
Funksjoner med flere variable som ikke forandres om en bytter om variablene.

Søylediagram
Viser en fordeling av data fra for eksempel en spørreundersøkelse. Høyden på en søyle vil da vise svarfrekvensen.
Se Stolpediagram

Tabell
Tabeller brukes til å organisere informasjon, ofte i kolonner og rader.
Eksempel: rutetabell for buss, resultatliste for skirenn
Tall
Begrep som i sin enkleste definisjon betyr antall og som skrives med siffer. Et litt mer utvidet tallbegrep omfatter også negative tall og brøker.
Tall på standardform
Se standardform
Tallfølge
En sekvens av tall, i en gitt rekkefølge.
Tallene kalles leddene i tallfølgen, og tallet kalles det -te leddet.

Tallinje
En rett linje der hvert punkt korresponderer til et tall og ethvert tall svarer til et punkt på linjen.
Tallmønster
Et tallmønster er en rekke med tall som er stillt opp i et bestemt system eller mønster, slik at man kan finne verdien av et tall så lenge vi kjenner til systemet/mønsteret og tallets plassering.
Tallpar
Beskriver plasseringen av et punkt i et koordinatsystem på formen (x, y).
Tangens
En trigonometrisk funksjon.
Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.

Tangent
Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Tellbar
En tellbar mengde er en mengde som kan avbildes med en-til-en korrespondanse med de naturlige tallene. En ikke tellbar mengde er en uendelig mengde.
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.

Tellestrek
Tellestreker bruker vi for å få en oversikt når vi teller opp antall. Det er lurt å gruppere fem og fem streker, slik at vi enklere får telt opp til slutt.

Terassepunkt
Et terassepunkt for en funksjon er et stasjonært punkt (et punkt der den deriverte er null), som verken er et topp- eller bunnpunkt.
Terning
Se Kube
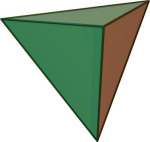
Tetraeder
Et legeme som begrenses av fire kongruente, likesidede trekanter.
Se Platonske legemer
Tideler
Sifferet som står på tidelsplassen i et desimaltall viser hvor mange tideler det er i tallet. Tidelene er den første desimalen.
Eksempel: Sifferet 7 står tidelsplassen i 4,72 og viser at tallet har 7 tideler.
Tidsenhet
Det grunnleggende tidsmålet er sekund. Andre tidsenheter er minutt, time og døgn.
Sammenhengen mellom tidsenhetene er ikke basert på 10-tallsystemet, slik vi er vant til fra lengde og vekt.
Tiere
Sifferet som står på tierplassen forteller hvor mange tiere det er i tallet.
Eksempel: 3847. Dette tallet har 4 tiere.
Tierovergang
Når summen av ensifrede tall blir større enn ti, får vi en tierovergang.
Todimensjonal
Betyr at vi har å gjøre med flater. Figurer som er todimensjonale (2D) har punkter i x- og y-planet, det vil si i to dimensjoner.
Sirkelen er todimensjonal, mens kula er tredimensjonal. Fotografier og TV-bilder er todimensjonale, selv om det er en tredimensjonal virkelighet som skal framstilles.

Topologi
Et felt i matematikk som studerer egenskaper ved figurer og flater som er uavhengig av kontinuerlige forandringer av størrelse og form.
Illustrasjonen er fra Wikimedia commons.
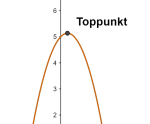
Toppunkt
Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
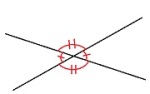
Toppvinkler
Når to rette linjer skjærer hverandre, dannes to par like store vinkler. Et slikt par kalles toppvinkler.
Torus
En torus er det ringformede omdreiningslegeme som framkommer ved at en dreier en sirkel 360° i rommet omkring en linje i dens plan med linjen utenfor sirkelen.
Overflaten er , og volumet er der er sirkelens radius og er avstanden fra sirkelens sentrum til omdreiningsaksen.
Transcendentalt tall
Et reelt tall som ikke er et algebraisk tall. For eksempel (pi) og e .
Transfinite tall
Et uendelig kardinaltall eller et uendelig ordinal. Aritmetikkens operasjoner med endelige kardinaltall kan utvides til en aritmetikk for transfinite. Denne har noen av den vanlige aritmetikkens egenskaper, men også noen forskjeller. F.eks. gjelder m+1=m og m+m=m for alle uendelige kardinaltall.
Transformasjon
En avbildning fra en mengde funksjoner til en mengde av funksjoner. Koordinattransformasjon og Laplace-transformasjon er to eksempler.
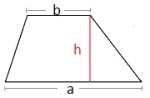
Trapes
Firkant der to sider er parallelle.
Areal =
Tredimensjonalt
Tredimensjonalt (3D) betyr at vi har å gjøre med rom. Til forskjell fra flater (2D), har rom også dybde, den tredje dimensjonen.
Sirkelen er todimensjonal, mens kula er tredimensjonal.

Trekant
En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
Trigonometri
Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.
Trigonometrisk rekke
En rekke der hvert ledd er en potens av en trigonometrisk funksjon.
Eksempel:
Trigonometriske funksjoner
Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.
Trigonometriske identiteter
En trigonometrisk identitet er to trigonometriske uttrykk som er like for alle verdier av de ukjente størrelsene. For eksempel er en trigonometrisk identitet. Det betyr at uttrykkene og 1 er identisk like for alle .
Tusenskille
Når vi skriver store tall, er det vanlig å sette inn et mellomrom for hvert tredje siffer. Mellomrommet kalles et tusenskille.
Eksempel: 2 434 765 000.
Tverrsum
Tverrsummen av et tall finner vi ved å addere sifrene i tallet. Kalles også siffersum.
Eksempel: 8483 har tverrsum 8 + 4 + 8 + 3 = 23.
Av og til har vi bruk for å finne minste tverrsum. Da fortsetter vi med å ta tverrsummen av resultatet helt til vi har et ensifret tall. 8483 har tverrsum 8 + 4 + 8 + 3 = 23, 2 + 3 = 5.
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
Uavhengige hendelser
To begivenheter A og B kalles uavhengige dersom utfallet i den ene ikke påvirker utfallet i den andre.
Uekte brøk
En brøk der teller er større enn eller lik nevner.
Eksempel: er en uekte brøk.
Uendelige mengder
En uendelig mengde inneholder et uendelig antall elementer. Primtallene danner en uendelig mengde.
Uendelige rekker
En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.
Eksempel :
( ∞ er tegnet for uendelighet )
Ukjent
I algebra brukes bokstaver for å betegne en ukjent størrelse. En ukjent størrelse kan være et tall som skal tilfredsstille en bestemt ligning.
Eksempel: x + 7 = 16. Her er x en ukjent.
Ulikhet
En ulikhet er et matematisk utsagn som sier at to størrelser har ulike verdier. Ulikheter kjennetegnes ved ulikhetstegn: .
a b, a er større enn b.
a b, a er mindre enn eller lik b.
a b, a er ulik b.
Uniform sannsynlighet
Sannsylighetsfordelingen i et utfallsrom kalles for uniform, hvis alle utfallene i utfallsrommet har like stor sannsynlighet for å inntreffe.
Eksempel: Kaster vi en mynt er det like stor sannsynlighet for å få mynt som kron. Kaster vi en terning er det like stor sannsynlighet for å få en 2-er som en 6-er.

Union
Unionen av to mengder A og B er en ny mengde som består av alle elementer som forekommer i minst en av A og B.
Eksempel: hvis er to mengder, blir unionen .
Uordnede utvalg
Når vi trekker objekter fra en samling og rekkefølgen vi trekker i ikke er viktig, sier vi at dette er et uordnet utvalg.
Eksempel: Lottotrekning.
Uten tilbakelegging
Dersom vi ikke legger tilbake den første gjenstanden før vi trekker neste, sier vi at et forsøk er gjort uten tilbakelegging.
Eksempel: Lottotrekning.
Utfall
Mulig resultat av en hendelse.
Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.
Utfallsrom
Alle mulige utfall en hendelse kan ha. Utfallsrom betegnes med .
Eksempel: Karakterer på en matematikkprøve har utfallsrommet .
Utfallstre
Se Valgtre
Utforsking
I matematikk er utforsking en måte å jobbe med mateamtiske problemstillinger på. Når man stadig stiller nye spørsmål ved problemet og selv kommer opp med mulige løsningsmetoder driver man med utforsking som aktivitet.
Utsagn
Et utsagn er en påstand som er sann eller usann.
Hvis det ikke er mulig å avgjøre om påstanden er sann eller usann, er den ikke et utsagn.
Eksempel: Januar har 30 dager. Påstanden er usann.
Utvalg
Et utvalg er en utvalgt og bestemt samling av personer som vi henter data fra. Utvalget er en representativ gruppe for populasjonen.
Utvide brøk
Å utvide en brøk betyr å multipliseres teller og nevner med samme tall. Brøken beholder samme verdi.
Eksempel: er utvidet til , fordi
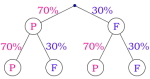
Valgtre
Gir oss oversikt over alle mulige kombinasjoner av utfall for en gitt hendelse.
Valgtre er det samme som utfallstre.
Valuta
Er pengeenheten eller mynten i et land. Hvert land har sin egen valuta.
Norske kroner (NOK) er den norske valutaen.
Valutakurs
Valutakursen forteller hvilken verdi pengene i to land har i forhold til hverandre.
Denne kursen bestemmes fra dag til dag i de enkelte land.
Variabel
En bokstavbetegnelse på et vilkårlig element i en mengde. Det motsatte er en konstant.
Eksempel: I uttrykket y = x + 3 er 3 en konstant og x en variabel. y er en annen variabel, avhengig av x.
Se Variable størrelser
Variable størrelser
Variable størrelser er vilkårlige, matematiske elementer i en mengde. Variabler betegnes som bokstavsymboler og brukes i likninger og funksjonsuttrykk for å beskrive sammenhengen mellom variabler eller faktorer.
Variable størrelser kan variere i motsetning til konstanter som er bestemte.
Eksempel:
- y = 2x. Her er 2 en konstant, x er en variabel og y er en variabel som avhenger av x.
Varians
Et mål for spredningen i et datamateriale, som er lik kvadratet av standardavviket.
Slik finner du varians:
Regn ut gjennomsnittet
Regn forskjellene mellom gjennomsnittet og hvert av tallene
Kvadrer forskjellene
Summer kvadrater av forskjellene
Divider summen med det totale antallet data
Variasjonsbredde
Variasjonsbredden i et datamateriale er differansen mellom den største verdien og den minste verdien.
Variasjonsregning
Studiet av maksimums- og minimumsverdier for funksjoner som har verdier som avhenger av en kurve eller en annen funksjon.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Vekt
Vekt er et daglig uttrykk for det vitenskapen kaller masse.
Massen måler vi med en vekt. Grunnleggende enhet er kilogram (kg).

Vektor
En vektor er en størrelse med en retning.
I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.
Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .
Vektorfunksjon
En vektorfunksjon er en funksjon av en variabel t som gir en vektor fra origo for hver t:
Vektorprodukt
Kalles også kryssprodukt. Vektorproduktet er definert mellom to vektorer i (dvs. to tre-dimensjonale vektorer), og gir en ny vektor i . Hvis og så er vektorproduktet definert algebraisk som . Denne vektoren står normalt på både og , og retningen er gitt ved høyrehåndsregelen. Lengden på vektoren er , der v er vinkelen mellom vektorene .
Vektorregning
Å regne med vektorer.
Velferdsteknologi
Velferdsteknologi er teknologiske hjelpemidler som har som mål og funksjon å øke tryggheten og mobiliteten til personer med nedsatt funksjonsevne. Ved hjelp av velferdsteknologien skal personer med spesielle funksjonsbehov få mulighet til klare seg mer på egenhånd og kunne delta mer i forskjellige typer aktiviteter.

Vendepunkt
Et vendepunkt for en funksjon er et punkt , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte fortegn.
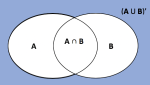
Venndiagram
Et venndiagram er en illustrasjon som beskriver en eller flere (del)mengder og forbindelsen mellom dem.
Eksempel: Mengde A er antall elever som spiller fotball og mengde B er antall elever som spiller håndball.
Det blå området viser elevene som verken spiller fotball eller håndball: A' ∩ B' = (A U B)'
Det hvite området beskriver unionen av A og B, mengden elever som spiller fotball, håndball eller begge deler: A U B.
Det hvite området mellom A og B er snittet av A og B, og viser til elever som spiller både fotball og håndball: A ∩ B.
Verdimengde
Mengden av verdier kan anta, kaller vi verdimengden til funksjonen.
Eksempel:
Det gir at har verdimengde fra og med 0 til og med 20.
Verditabell
En tabell med verdier av en variabel, for eksempel , og tilhørende funksjonsverdier, for eksempel , kalles for en verditabell.
Verditabellen gir oss oversikt over verdier som hører sammen. Den hjelper oss enten med å finne punkter som ligger på grafen til en funksjon eller funksjonsuttrykket til en graf.
Vinkel
En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.
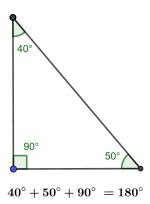
Vinkelsum
Summen av alle vinklene i en mangekant.
Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader.
Volum
Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
x-akse
Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.

y-akse
Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
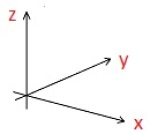
z-akse
Vanlig betegnelse på den tredje aksen i et koordinatsystem.
Økonomisk modell
En økonomisk modell uttrykker økonomiske sammenhenger som et system av ligninger. Ved å forenkle virkeligheten kan man ved å bruke økonomiske modeller forsøke å beregne fremtidig økonomisk aktivitet eller forklare sammenhenger mellom økonomiske størrelser.
Å sette prøve
Å sette prøve på en utregning betyr at vi kontrollerer om svaret er korrekt.
Vi kan for eksempel sette prøve på subtraksjoner og divisjoner ved å bruke de motsatte regnemåtene, addisjon og multiplikasjon eller vi kan sette prøve på en ligning.
Eksempel 1:
Eksempel 2:
Setter prøve på svaret:
Høyre side: 2x + 2 = 20 + 2 = 22
Venstre side: 4x – 18 = 40 – 18 = 22
Høyre side = venstre side




