abc-formelen

Vi har lært oss kvadratsetningene, vi vet hvordan vi fullfører kvadrater og vi har sett hvordan vi kan løse andregradslikninger ved å faktorisere dem. Nå skal vi lære en formel som gir oss løsningene direkte, og vise hvordan vi kan skrive et andregradsuttrykk ved hjelp av løsningene det har.

Hvis man starter med uttrykket $a x^{2} + b x + c$ og faktoriserer det slik vi så på i forrige del av lynkurset kan man utlede en generell sammenheng mellom koeffisientene og de x-verdiene som løser $a x^{2} + b x + c = 0$ . Vi skal ikke ta med utledningen her, men den er en fin oppgave å prøve å få den til – man fullfører et kvadrat, samler alt annet på andre side av likhetstegnet og tar så kvadratroten på begge sider og rydder opp.

Nok prat - her er $a b c$ -formelen:

Teorem. Løsningsformelen for andregradslikninger

La a, b og c være reelle tall, der $a \neq 0$ . Likningen $a x^{2} + b x + c = 0$ har løsningene

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

forutsatt at $b^{2} - 4 a c \geq 0$ . Dersom $b^{2} - 4 a c < 0$ har likningen ingen reelle løsninger.

Utledning av formelen

Vi skal bruke kvadratsetningene på en smart måte for å utlede formelen.

Vi divider med $a$ begge sider av likningen:

$a x^{2} + b x + c = 0$

$\frac{a x^{2}}{a} + \frac{b x}{a} + \frac{c}{a} = 0$

$x^{2} + \frac{b x}{a} + \frac{c}{a} = 0$

Nå ordner vi likningen slik at vi kan bruke

Første kvadratsetning

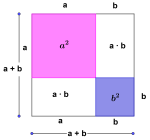
Første kvadratsetning sier at

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .

første kvadratsetning

. Trekk

\frac{c}{a}

fra begge sider av likningen. Da får vi

x^{2} + \frac{b}{a} x = - \frac{c}{a}

Husk første kvadratsetning:

$x^{2} + 2 t x + t^{2} = {(x + t)}^{2}$

Tenk på $\frac{b}{a}$ som $2 t$ eller $t = \frac{b}{2 a}$ . Legger vi til leddet $t^{2} = \frac{b^{2}}{4 a^{2}}$ på begge sider i likningen, får vi at venstresiden er et fullstendig kvadrat:

$x^{2} + 2 \frac{b}{2 a} x + \frac{b^{2}}{4 a^{2}} = \frac{b^{2}}{4 a^{2}} - \frac{c}{a}$

Uttrykket til venstre for likhetstegnet skrives om til

$x^{2} + 2 \frac{b}{2 a} x + \frac{b^{2}}{4 a^{2}} = {(x + \frac{b}{2 a})}^{2}$

Uttrykket til høyre for likhetstegnet settes på en felles brøkstrek,

$\frac{b^{2}}{4 a^{2}} - \frac{c}{a} = \frac{b^{2} - 4 a c}{4 a^{2}}$

Hele likningen er nå

${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$

Vi tar kvadratroten på begge sider av likhetstegnet:

$x + \frac{b}{2 a} = \pm \sqrt{\frac{b^{2} - 4 a c}{4 b^{2}}}$

Merk at vi må ta med både det positive og negative uttrykket fordi vi tar kvadratroten og dermed står det pluss-minus forran rottegnet. Trekk $\frac{b}{2 a}$ fra begge sider av likningen, og vi er i mål:

$x = \frac{- b}{2 a} \pm \frac{\sqrt{b^{2} - 4 a c}}{2 a} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Vi har altså funnet at $x$ kan ha maksimalt to løsninger, og de er gitt ved formelen:

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
Dersom uttrykket under rottegnet blir negativt, har likningen ingen reelle tall som løsning.

Uttrykket $b^{2} - 4 a c$ kalles diskriminanten til andregradslikningen. Antall løsninger er avhengig av om dette tallet er lik 0, er positivt eller er negativt (fortegn er en viktig egenskap ved et tall!):

$b^{2} - 4 a c = 0$ : Én løsning. Denne finner vi ved å gjenkjenne et fullstendig kvadrat eller eventuelt bruke abc-formelen.
$b^{2} - 4 a c > 0$ : To løsninger. Disse finner vi ved å bruke abc-formelen, eventuelt fullføre kvadratet som vi gjorde i forrige del av lynkurset (det siste er tidkrevende, men veldig tilfredsstillende med hensyn på algebrakunnskaper og forståelse).
$b^{2} - 4 a c < 0$ : Ingen løsning. abc-formelen gir at vi skal ta kvadratroten av et negativt tall, noe vi ikke kan. Forsøk på å fullføre kvadratet fører ikke frem, siden vi vil få et plusstegn der vi trenger et minustegn for å bruke konjugatsetningen.

Et spesialtilfelle av formelen kan være verdt å merke seg. Dersom likningen vi skal løse er på formen

x^{2} + 2 b x + c,

der $b$ og $c$ er reelle tall, får vi en ekstra ﬁn formel for løsningene:

x = \frac{- 2 b \pm \sqrt{{(2 b)}^{2} - 4 c}}{2} = \frac{- 2 b \pm 2 \sqrt{b^{2} - c}}{2} = - b \pm \sqrt{b^{2} - c}

Å bruke abc-formelen er ganske rett fram, men vi tar med noen eksempler. Vi oppfordrer å regne over selv, så du er sikker på at du skjønner hvordan formelen brukes.

Eksempel 1

Løs likningen $x^{2} + x - \frac{3}{4} = 0$ .

Her kan vi bruke den noe enklere formelen, med $b = \frac{1}{2}$ , $c = - \frac{3}{4}$ . Da får vi med en gang at svaret er

x = - \frac{1}{2} \pm \sqrt{{(- \frac{1}{2})}^{2} - (- \frac{3}{4})} = - \frac{1}{2} \pm \sqrt{\frac{1}{4} + \frac{3}{4}}

og det betyr at løsningene til likningen er $x = - \frac{3}{2}, x = \frac{1}{2}$ .

Eksempel 2

Løs likningen ${2 x}^{2} - 4 x + \frac{3}{2} = 0$ .

Her har vi $a = 2$ , $b = - 4$ og $c = \frac{3}{2}$ . Når vi setter dette inn i abc-formelen får vi de to løsningene

x = \frac{4 \pm \sqrt{16 - 12}}{4} = \frac{4 \pm 2}{4} = {\begin{matrix} \frac{3}{2} \\ \frac{1}{2} \end{matrix} .

Vi får to løsninger, som er det vi venter oss med positiv diskriminant.

Eksempel 3

Løs likningen ${2 x}^{2} + 7 x + 7 = 0$ .

Her er diskriminanten $7^{2} - 4 \cdot 2 \cdot 7 = 49 - 56 = - 7 < 0$ , og dermed har ikke likningen noen løsninger.

Eksempel 4

Løs likningen $x^{2} + 9 = - 6 x$ .

Dette er det samme som å løse $x^{2} + 6 x + 9 = 0$ , og selv om vi kan gjøre dette med abc-formelen er det enda lettere å huske at ved 1. kvadratsetning er

x^{2} + 6 x + 9 = {(x + 3)}^{2}

og av det ser vi at $x = - 3$ er eneste løsning. Sjekk gjerne selv at diskriminanten faktisk er 0.

Eksempel 5

Løs likningen $e^{2 x} + {2 e}^{x} - 8 = 0$ .

Setter vi

u = e^{x}

blir likningen omskrevet til

u^{2} + 2 u - 8

. Formelen gir da at

u = - 1 \pm \sqrt{1 + 8} = - 1 \pm 3

\Rightarrow

u = - 4

eller

2

For å finne

x

, må vi nå løse likningene

e^{x} = - 4

e^{x} = 2

. Den første av disse har ingen løsning, siden

e^{x}

alltid er positiv. Den andre løser vi på vanlig måte:

tekst

e^{x} = 2

\Leftrightarrow

x = \ln 2.

Den opprinnelige likningen har derfor

x = \ln 2

som eneste løsning.

Faktorisering av andregradsuttrykk

Nå har vi sett på mange eksempler på hvordan vi kan løse andregradsuttrykk. La du merke til at i eksempel 4 over kunne vi skrive uttrykket på en slik måte at vi så med en gang hva som var løsningene? Dette kan man faktisk gjøre generelt, og vi har at følgende regel gjelder:

Teorem. Faktorisering av andregradsuttrykk

La a, b og c være reelle tall, der $a \neq 0$ , og anta at likningen ${a x}^{2} + b x + c = 0$ har løsningene $x_{1}$ og $x_{2}$ . (Disse kan være like). Da har vi faktoriseringen

$a x^{2} + b x + c = a (x - x_{1}) (x - x_{2}) .$

Eksempel 6

Faktoriser uttrykket $x^{2} + x - \frac{3}{4}$ ved å bruke teoremet.

Dette uttrykket kjenner vi løsningene til fra eksempel 1 over, så vi kan bruke teoremet rett fram og ser at $x^{2} + x - \frac{3}{4} = (x + \frac{3}{2}) (x - \frac{1}{2})$ . Prøv gjerne å gange ut igjen selv for å se at dette stemmer.

Del på Facebook

Del på Facebook

Begrep

abc-formelen

abc-formelen sier at en likning på formen $a x^{2} + b x + c = 0$ har løsningene $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .
Diskriminant

For en andregradslikning $a x^{2} + b x + c = 0$ kalles tallet $b^{2} - 4 a c$ for diskriminanten. Om dette tallet er negativt har likningen ingen løsninger, om det er 0 har den én, og om det er positivt har likningen to løsninger.
Første kvadratsetning

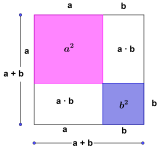
Første kvadratsetning sier at

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .

abc-formelen

Utledning av formelen

Første kvadratsetning

Eksempel 1

Eksempel 2

Eksempel 3

Eksempel 4

Eksempel 5

Faktorisering av andregradsuttrykk

Eksempel 6

Begrep

abc-formelen

Diskriminant

Første kvadratsetning