Ettpunktsformelen og likning for tangentlinjen
Når vi kjenner den deriverte til en funksjon, er det en enkel sak å finne likningene for
Tangent
Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
|
Teorem. Ettpunktsformelen . |
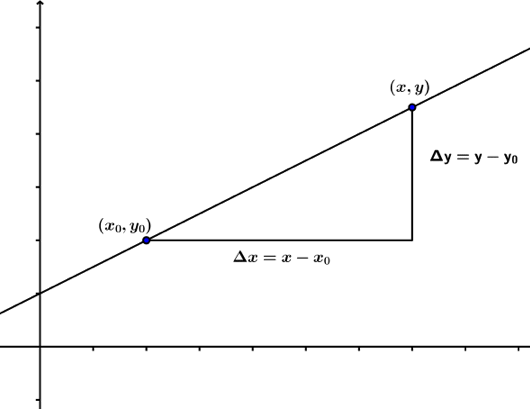
Bevis. La være et vilkårlig punkt på , forskjellig fra (se figuren under). Siden stigningstallet til en linje er lik , får vi sammenhengen
| det vil si |
Ganger vi opp med nevneren , får vi formelen i teoremet over.
La oss nå vende tilbake til graftangenter. Anta at er en deriverbar funksjon, og la være et punkt på grafen. Vi skal finne tangenten i dette punktet. Men stigningstallet til tangenten er jo verdien av den deriverte! Vi skal altså ha tak i likningen for linja som går gjennom punktet , og har stigningstall . Svaret følger rett fra ettpunktsformelen:
| Teorem. Likning for tangentlinje
|
Eksempel
Oppgave. Finn tangenten til grafen til i punktene og .
Løsning. Vi setter rett inn i formelen i teoremet over, med . I det første punktet er , og vi får tangentlikninga
| . |
I det andre punktet har vi , og vi får tangenten
| . |
(Sjekk mellomregningene selv hvis du er usikker.)
Del på Facebook