Faktorisering av andregradsuttrykk
Vi har nå lært hvordan vi bruker kvadratsetningene og hva et fullstendig kvadrat er. Dette skal vi nå sette sammen og bruke til å faktorisere generelle andregradsuttrykk.
Det er lettere å faktorisere uttrykk der , og faktisk trenger vi ikke å faktorisere andre uttrykk. Det kan vi se, siden
| , |
og dermed holder det å faktorisere uttrykket . Den beste måten å gjøre det på er via å fullføre kvadratet.
For å gjøre det litt leselig viser vi metoden på et eksempel. Vi prøver å faktorisere følgende andregradsuttrykk:
Dette uttrykket minner om høyresiden i 2. kvadratsetning, men hvis vi prøver å få tallene til å passe ser vi at det ikke går an. Vi prøver å skrive det som for en eller annen d, og ser at for å fullføre kvadratet må vi ha konstantleddet 16. Da kan vi regne som følger.
| vi legger til , som er lov | |
| de tre første leddene er et fullstendig kvadrat | |
| 2. kvadratsetning | |
| litt heldige med 9-tallet siden | |
| 3. kvadratsetning! | |
Dette gir oss faktoriseringen
Grunnen til at vi kunne bruke 3. kvadratsetning i eksempelet over er at det står minustegn foran 9-tallet. Ikke alle uttrykk vil gi et minustegn (eller et 9-tall for den saks skyld) på denne plassen: Hvis vi får et plusstegn her, betyr det at uttrykket ikke kan faktoriseres.
Det er verdt å få med seg at nå som vi har faktorisert uttrykket er det ganske lett å løse likningen
| . |
Vi fant jo at
| , |
og for at dette uttrykket skal være 0, må minst en av faktorene og være . Da ser vi at løsningene må være eller (sjekk dette ved å sette inn i andregradsuttrykket!)
Del på Facebook
Begrep
-
Andre kvadratsetning
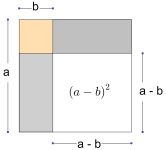
Andre kvadratsetning sier at
.
-
Andregradsuttrykk
Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.
-
Konjugatsetningen
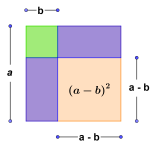
Konjugatsetningen kalles også tredje kvadratsetning:
.




