Hopp til hovedinnholdet
www.matematikk.org

Gjennomsnitt, median og typetall

Når vi jobber med et stort datasett klarer vi ikke å holde alle observasjonene i hodet. Derfor lønner det seg ofte å beregne sentralmål. De gir blant annet en viss følelse for hvilken verdi observasjonene ligger rundt, og hva den mest «normale» verdien er blant dataene. Gjennomsnittet, medianen og typetallet er de tre mest brukte sentralmålene i statistikken.

Gjennomsnitt

definisjon

Gjennomsnittet er middelverdien av alle dataene.

Det finner du ved å summere alle dataene og dividere summen på det totale antall data.

Median

definisjon

Medianen finner vi ved først å sortere alle dataene i stigende rekkefølge, og finne det midterste tallet.

Hvis antall data er oddetall, er medianen det midterste tallet. Men hvis antall data er partall, må vi først finne de to midterste tallene, og regne ut gjennomsnittet av disse. Dermed er medianen det tallet i dataene som gjør at halvparten av observasjonene er mindre enn det og den andre halvparten er større.

Typetall

definisjon

Typetallet er den mest «typiske» observasjonen i en datasamling, og det er det tallet som forekommer flest ganger.

Typetallet er den observasjonen med flest forekomster i frekvenstabellen, den høyeste søylen i søyle- eller stolpediagrammet, eller den største sektoren i sektordiagrammet.

Merk at typetallet ikke behøver være et tall. Hvis dataene ikke er numeriske, kan typetallet for eksempel være en bokstav.

To eksempler

La oss se på et par eksempler på hvordan vi finner sentralmålene i praksis.

En treg dusjer

Pernille har fått høre av søskene sine at hun bruker lang tid på badet. Hun noterte ned tiden hun brukte i dusjen i en uke (i minutter), og de er

 36   42   29   35   38   32   42   (min) 

Gjennomsnittstiden er

36+42+29+35+38+32+427=36,3≈36⁢ minutter.

Vi sorterer dataene etter størrelse og får:

 29   32   35   36   38   42   42   (min) 

Siden antall data er oddetall, blir medianen det midterste tallet, nemlig 36 minutter.

I dette eksemplet ser vi at gjennomsnittet og median sammenfaller med hverandre, men vanligvis er ikke det tilfellet – gjennomsnittet blir mye mer påvirket av om det er med noen veldig store eller veldig små tall blant dataene.

Til slutt observerer vi at typetallet er 42 (minutter), siden Pernille dusjet i 42 minutter to ganger.

Antall besøk i Frankrike

I en undersøkelse ble 20 elever spurt hvor mange ganger Bildet er hentet fra parisinfo.com

de har vært i Frankrike. Dataene ser slik ut, der tallet angir hvor mange ganger hver elev har vært i Frankrike:

 1   0   2   1   0  3   0   2   2   0 
 0  0   2  0  0  1  0   1  3   0

 

 

 

Gjennomsnittet er 

 1+0+2+1+0+3+0+2+2+0+0+0+2+0+0+1+0+1+3+020=0,9≈1.

Gjennomsnittet sier at en typisk elev "nesten" har vært i Frankrike én gang, men faktisk har halvparten av elevene aldri vært der. Dette viser at gjennomsnittet påvirkes mye av de som har vært der mer enn én gang.

Dataene ordnet i stigende rekkefølge ser slik ut:

 0   0   0   0   0   0   0   0   0   0 
 1   1  1   1   2   2   2   2   3   3


 

 

Vi har totalt 20 data, altså et partall. Median er gjennomsnittet av de to midterste tallene, 0 og 1, altså

 0+12=0,5.

Siden de fleste dataene er 0, er typetallet lik 0.

Dette eksemplet forteller oss at selv om både gjennomsnitt, median og typetall kalles sentralmål, ligger de ikke nødvendigvis i nærheten av hverandre. Det å velge hvilke sentralmål man vil bruke for å få best oversikt over dataene sine krever innsikt og forståelse.

Del på Facebook

Del på Facebook

Begrep

  • Frekvenstabell

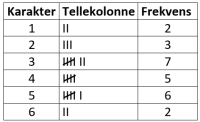
    Frekvenstabell

    En frekvenstabell er en opptelling og ordning av dataene i en datasamling.

    Se frekvens

  • Gjennomsnitt

    Gjennomsnitt er en middelverdi av alle dataene.

    Gjennomsnittet finner du ved å:
    1) summere alle data
    2) dele summen på total antall data

    Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
    1) 2+2+4+3=11
    2) antall data er 4.  11:4=2,75

  • Ikke-numeriske data

    Data som ikke er tall, for eksempel bokstaver, farger og gjenstander.

  • Median

    Medianen er den verdien som vi finner i midten av et rangert datamateriale.

    Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.

  • Sektor

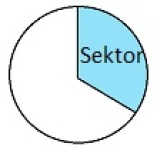
    Sektor

    En sektor er en del av en sirkel, et område som er avgrenset av to radier og en sirkelbue. En sektor har form som et kakestykke.

  • Sektordiagram

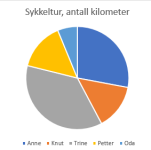
    Sektordiagram

    Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.

     

  • Sentralmål

    Sentralmål er utregnede verdier som viser "sentrum" for innsamlede data. Tre eksempler på sentralmål er gjennomsnitt, median og typetall.

    Se gjennomsnitt, median og/eller typetall

  • Søylediagram

    Søylediagram

    Viser en fordeling av data fra for eksempel en spørreundersøkelse. Høyden på en søyle vil da vise svarfrekvensen.

    Se Stolpediagram

  • Typetall

    Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.

    Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.

Hopp over bunnteksten