De viktige tallmengdene
Tallmengdene vi bruker som oftest er: naturlige tall, heltall, rasjonale tall, irrasjonale tall og reelle tall.
Tallmengder fra MatRIC
Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC
Naturlige tall
De naturlige tallene kan sies å være den mest grunnleggende tallmengden. De kalles også telletallene, siden de er tallene som brukes til opptelling:
Når vi skriver prikker på slutten, betyr det at tallene som kommer etter følger samme mønster som de vi allerede har satt opp. Mengden av de naturlige tallene har fått et standardsymbol: en stor, uthevet ℕ. Vi skriver
ℕ = {1, 2, 3, 4, 5, 6, …}.
Det er uendelig mange naturlige tall. En fundamental egenskap ved dem er nemlig at ethvert naturlig tall har en etterfølger som er et naturlig tall. Altså, samme hvor stort tall vi tenker på, kan vi alltid finne et større ved å legge til én. Til dette nye tallet kan vi også legge til én, og slik kan vi fortsette.
Heltall
Hvis vi tar utgangspunkt i de naturlige tallene, og i tillegg tar med de negative tallene samt tallet null, får vi den tallmengden som kalles de heltallene. Heltallene har, i likhet med de naturlige tallene, et fast symbol som angir dem: en stor, uthevet ℤ.
ℤ = {... , -2, -1, 0, 1, 2, 3, ...}
Vi legger merke til at de naturlige tallene er inneholdt i heltallene. Med symboler:
ℕ ℤ
Dette leses: Mengden ℕ, som er de naturlige tall, er en delmengde av mengden ℤ, mengden av alle heltall.
Rasjonale tall
Mengden som består av alle heltall og alle tall som kan skrives som en brøk der både teller og nevner er hele tall, kalles rasjonale tall. Heltallene er en delmengde av de rasjonale; vi kan jo også alltid skrive et helt tall n som . De rasjonale tallene har fått symbolet ℚ.
Vi noterer oss:
ℕ ℤ ℚ
Man kan uttrykke de rasjonale tallene som en mengde ved hjelp av mengdeklammer:
Vi leser: De rasjonale tallene ℚ er mengden av alle brøker , der a og b er heltall, og b er ulik 0.
Skrivemåten (a, b) ℤ er en kortform for a ℤ og b ℤ.
Irrasjonale tall – reelle tall
Noen tall kan ikke skrives som brøk. For eksempel er det ikke mulig å skrive eksakte uttrykk for eller for som brøk. Vi tar med et resonnement som viser at tanken om som en brøk vil føre til en selvmotsigelse, og derfor er umulig:
Vi forestiller oss at , og at denne brøken er forkortet så mye som mulig (hvis den ikke er forkortet, kunne vi jo bare gjøre det før vi begynte). Det betyr at for eksempel 2 ikke kan være faktor i både a og i b.
Nå, hvis , må vi ha . Så kvadrerer vi denne likningen og får . Det betyr at a2 er et partall, og da må a selv være et partall.
Sett . Det gir , altså . Da kan vi forkorte med 2, og får , som viser at også b er et partall. Men da har a og b likevel en felles faktor, 2, som var imot forutsetningen at var forkortet mest mulig.
Antikkens grekere var sannsynligvis de første til å finne irrasjonale tall. Tallet dukket opp som diagonalen i et kvadrat med sidekanter lik 1 (jf. Pytagoras’ setning).
Tallet , som alle andre irrasjonale tall, er et tall som ikke kan skrives som en brøk, og dermed heller ikke som et endelig desimaltall. Vi kan likevel tilnærme irrasjonale tall med desimaltall så nøye vi skulle trenge, ved bare å ta med et tilstrekkelig antall desimaler. Vi kan som en kuriositet ta med denne tilnærmelsen til tallet :
Det er ikke noe system, for eksempel ingen periodisitet, i utviklingen av desimalene for , og heller ikke for andre irrasjonale tall. Vi kan aldri forutsi hva som blir den neste desimalen uten å regne den ut – og det kan være komplisert. Det betyr at vi aldri kan uttrykke helt eksakt ved hjelp av desimaltall. Det samme gjelder alle irrasjonale tall. Rasjonale tall kan derimot alltid uttrykkes enten som et avsluttet desimaltall, eller et desimaltall der desimalutviklinga vil gjenta seg med en periodisitet.
Eksempler:
I første tilfellet ser vi at perioden 571428 vil gjenta seg i det uendelige.
De irrasjonale tallene er like ”ekte” tall som de rasjonale tallene. Et kvadrat med sidekanter 1 har jo en diagonal, og diagonalen må selvsagt ha en lengde. Vi klarer bare ikke å uttrykke lengden eksakt med desimaltall eller brøker.
Vi oppsummerer: Det fins uendelig mange naturlige tall. Det fins også uendelig mange heltall i tillegg til de naturlige, og de naturlige tallene er en delmengde av heltallene. I tillegg fins uendelig mange rasjonale tall som ikke er hele, og heltallene er en delmengde av de rasjonale. Til sist fins uendelig mange irrasjonale tall. Til sammen utgjør alle disse tallene, de rasjonale og de irrasjonale, alle tallene vi finner på tallinja, og denne komplette tallmengden kalles de reelle tallene. Symbolet for denne tallmengden er en stor, uthevd ℝ.
De reelle tallene er unionen av de rasjonale og de irrasjonale tallene
ℝ =ℚ {Alle irrasjonale tall}
(Det fins ikke noe eget symbol for de irrasjonale tallene).
Og vi har denne sammenhengen, som viser hvordan tallmengdene er utvidelser av hverandre:
ℕ ℤ ℚ ℝ
Eksempler – tall i tallmengdene
Vi vil bestemme hvilke tallmengder følgende åtte tall tilhører:
For det første: De reelle tallene omfatter alle tall vi beskjeftiger oss med, og derfor er alle disse åtte tallene reelle. Så vi vil endre spørsmålet til: Finn den minste eller snevreste av tallmengdene foran som hvert enkelt av de åtte tallene tilhører.
- Tallet 1 er et naturlig tall. Vi skriver: ℕ .
- Tallet har vi diskutert under irrasjonale tall, og derfor kan vi si direkte at er irrasjonal, ℝ.
- kan vi regne ut. , som er et positivt heltall, dvs. et naturlig tall. ℕ.
- kan vi også regne ut. , som også er et naturlig tall. ℕ.
- er ikke et heltall, men en brøk med heltallig teller og nevner. Derfor er et rasjonalt tall. ℚ.
- 0 er et heltall. ℤ. (I enkelte sammenhenger tar noen med 0 blant telletallene, men vi gjorde ikke det her).
- er ikke rasjonal. er et irrasjonalt tall, og dersom vi deler et irrasjonalt tall på 2, får vi fortsatt et irrasjonalt tall. ℝ.
- 7,05 er ikke et heltall. Vi kan derimot skrive 7,05 som en brøk, . Vi ser derfor at 7,05 er et rasjonalt tall: ℚ.
Del på Facebook
Begrep
-
Naturlige tall
De positive heltallene 1, 2, 3, 4...
Mengden av naturlige tall angis med symbolet .
Hvis 0 skal være med i mengden bruker vi symbolet .
-
Heltall
Heltall er de tallene vi oftest teller: 0, 1, 2, 3, 4... De hele tallene inkluderer også de negative tallene; -1, -2, -3...
Symbolet for mengden av hele tall er ℤ.
-
Rasjonale tall
Et tall som kan skrives som en brøk på formen der m og n er hele tall og n forskjellig fra 0. Mengden av rasjonale tall er ℚ.
Eksempel:
0,42, kan skrives som
2, kan skrives som
-
Brøk
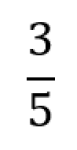
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Irrasjonale tall
Et reellt tall som ikke kan skrives som en brøk satt sammen av to heltall.
Eksempel: ,
-
Reelle tall
Tall som kan markeres på en tallinje. Mengden av reelle tall er ℝ.
Eksempel: Alle heltall, alle rasjonale tall og alle irrasjonale tall.
-
Pi (π)
er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.




