Tallet e

Tallet som i dag kalles e opptrer for første gang i et brev skrevet i 1690 av Leibniz, men da med notasjonen b. Det var i et annet brev, skrevet av Euler i 1731, at notasjonen e ble brukt for første gang for tallet som er tilnærmet lik 2,71828. Noen mener at e står for "eksponentiell", siden tallet e er det naturlige valget til grunntall i en eksponentialfunksjon, mens andre mener at Euler brukte e siden det er den andre vokalen i alfabetet og siden han allerede brukte a i noen av sine andre matematiske arbeider.

Akkurat som tallet π, som er tilnærmet 3,14159, er også tallet e et irrasjonalt tall, men å regne ut desimaler for e har aldri blitt like populært som å regne ut desimaler for π. Vi ser også av årstallene vi har nevnt at e var en nykommer i forhold til π. Men selv om tallet e ikke hadde noen notasjon før mot slutten av 1600-tallet, opptrådte det allikevel i matematiske arbeider på hele 1600-tallet uten å bli identifisert. Da tallet ble identifisert, ble disse arbeidene viktige i forståelsen av tallet. Til disse arbeidene hører Napiers arbeider om logaritmer (1618), Huygens’ arbeider med rektangulære hyperbler, eksponentialkurven og logaritmer (1661) og ikke minst Bernoullis arbeid med grensen av uttrykket ${(1+\frac{1}{n})}^n$ når n går mot uendelig (1683).

I prosessen med å forstå tallet e skjønte man raskt at dette var nært knyttet til logaritmer. I de første arbeidene innen logaritmeteori var logaritmer tall som gjorde regningen lettere. I dag tenker vi på logaritmen med grunntall a av det positive tallet b som det tallet vi må opphøye a i for å få b, skrevet $a^{{\log }_{a}b}=b$. Dessuten tenker vi på logaritmer som funksjoner med tilhørende eksponentialfunskjoner der disse er inverse funksjoner. Og vi vet at e er grunntallet i den naturlige logaritmen, dvs. $e^{\ln \left(b\right)}=b$. Erstatter vi b med en bokstav lengre ut i alfabetet, får vi funksjonen $e^{\ln \left(x\right)}=x$, x > 0.

Det som gjør at e er grunntallet i den naturlige logaritmen er følgende egenskap:

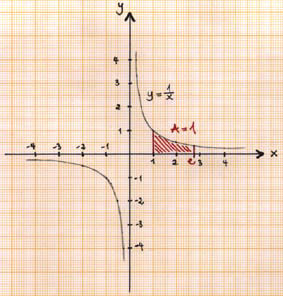
Hvis vi tegner funksjonen $y=\frac{1}{x}$, får vi en rektangulær hyperbel. Ordet rektangulær kommer av at når x og y er positive, er de lengdene på sidene i et rektangel med areal 1. Tallet e er nå tallet slik at arealet under den rektangulære hyperbelen fra 1 til e er 1:

Skrevet med dagens integrasjonsnotasjon:
${\int }_1^e\frac{1}{x}dx={[\ln (x)]}_1^e=1$

Vi nevner til slutt noen flere egenskaper ved e:

Egenskap 1)  $e=\underset{n\to \infty }{\lim }{(1+\frac{1}{n})}^n$

Egenskap 2)  $e=\sum _0^{\infty }\frac{1}{n}!$

Begge disse ble funnet av Euler. Egenskap 2) sier at e kan uttrykkes ved en uendelig rekke. Denne kan blant annet brukes til å regne ut desimaler for e og til å vise at tallet e er irrasjonalt. En tredje egenskap gjelder eksponentialfunksjoner a^x: Hva må grunntallet a være for at hastigheten funksjonen vokser med i hvert punkt er lik funksjonsverdien i punktet? Jo, grunntallet må være e:

$f\left(x\right)=e^x$
$f^{\prime }\left(x\right)=e^x$

Det fins mange formler som involverer e, og i artikkelen om tallet i finner du en formel som knytter sammen tallene π og e! Men for eksempel differansen π - e, som er ca. 0,42331, har ikke vært utforsket i særlig grad… Er dette et tall som dukker opp i noen interessante sammenhenger?